图的存储

搜索与图论

数据结构 空间
DFS stack O(n)
BFS queue 最短路

DFS

  • 采用stack
  • 回溯——恢复状态
  • 剪枝——提前回溯

遇到诸如放置、字典序等可使用深搜输出全部组合。

BFS

  • 采用queue
  • 边权都为1时，为最短路径
  • DP是特殊的最短路问题

acwing842 ——DFS

image-20240709120409519

从0开始进行深搜（不从1开始是因为1也要进行排序）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>

using namespace std;

const int N = 100;

int n;  //记录深度

int path[N];
int st[N];

void dfs(int u)
{
    if (u== n)  
        {
            for (int i = 0 ;i < n; i ++)
            printf("%d", path[i]);
            puts("");
            return;
        }
    for (int i = 1; i <= n; i ++)
        {
            if(!st[i])
                path[u] = i;
                st[i] = true;
                dfs(u + 1);
                st[i] = false;
        }
}


int main()
{   
  
    cin >> n;
  
    dfs(0);
    
    return 0;
}

acwing843 ——DFS

通过枚举每行（若n皇后问题能解决，则每行必有一个皇后），再通过行表示列和对角线（计算不能放置的位置，如该行某点放置则该点列不能放置），判断条件符合则递归调用dfs。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>


using namespace std;
const int N  = 200; 
int n;
char g[N][N];

bool col[N], dg[N], udg[N];
//列    column
//行    line
//对角线    diagonal


void dfs(int u)
{
    if (u == n)  
        {
            for (int i = 0 ;i < n; i ++)    puts(g[i]); //char* 型指针
            puts("");
            return;
        }
    for (int i = 0; i < n; i ++)       //枚举列
        {
            if(!col[i] && !dg[u + i] && !udg[n - u + i])
               { 
                g[u][i] = 'Q';
                col[i] = dg[u + i] = udg[n - u + i] = true;
                dfs(u + 1);
                col[i] = dg[u + i] = udg[n - u + i] = false;
                g[u][i] =  '.';
               }
        }
}


int main()
{
 
    cin >> n;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n; j ++)
            g[i][j] = '.';
    dfs(0);
    return 0;
}

acwing844 ——BFS

BFS算法相当于在有m个后继点的点处分裂为m个小鼠，同时将访问过的点在数组上标定距离（该距离是最小值，因为其他点在相同步数下并不能访问该点），最后返回要求的坐标即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 110;

typedef pair<int, int> PII;


int n, m;			//最终点
int g[N][N];        //存放数组
int d[N][N];        //到任意可达点的最短路径

PII q[N * N];



int bfs()
{
    int hh = 0, tt = 0;     //队头和队尾
    q[0] = {0, 0};      //起始点

    memset(d, -1, sizeof d);		//设置为为走过的路
    d[0][0] = 0;        //起始点距离为0

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};			//定义四个方向
    while (hh <= tt)
    {
        auto t = q[hh ++ ];
        for (int i = 0; i < 4; i ++ )		//往四个方向走
            {
                int x = t.first + dx[i], y = t.second + dy[i];
                if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1 )
                        {
                            d[x][y] = d[t.first][t.second] + 1;  //存储距离
                            q[ ++ tt] = {x,y} ;    //新建小鼠
                        }
            }
    }

    return d[n - 1][m - 1];
    
}




int main()
{   
 
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
        for (int j = 0;j < m; j ++ )
                cin >> g[i][j];

    cout <<  bfs()   << endl;     
    return 0;
}

acwing845 ——BFS

这题我们从输入的状态出发，直到到达最终的状态，本质是bfs算法，通过枚举所有可能的变换，在变换的基础上再进行枚举，直到匹配最终状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <queue>
#include <string>
#include <unordered_map>
using namespace std;

string finnal = "12345678x";
unordered_map<string, int> un_map; //存放状态
queue<string> status;              //存放小鼠

int bfs(string st) {
  un_map[st] = 0;
  status.push(st);

  int xway[4] = {-1, 0, 1, 0};
  int yway[4] = {0, -1, 0, 1};

  while (status.size()) {
    string tmp = status.front();
    status.pop();
    int pos = tmp.find('x');
    int x = pos / 3;
    int y = pos % 3;
    int distance = un_map[tmp];
    if (tmp == finnal)
      return distance;

    for (int i = 0; i < 4; i++) {
      int a = x + xway[i], b = y + yway[i];
      if (a >= 0 && a < 3 && b >= 0 && b < 3) {
        swap(tmp[pos], tmp[3 * a + b]);
        if (!un_map.count(tmp)) {
          un_map[tmp] = distance + 1;
          status.push(tmp);
        }
        swap(tmp[pos], tmp[3 * a + b]); //恢复现场
      }
    }
  }
  return -1;
}

int main() {
  string st;
  for (int i = 0; i < 9; i++) {
    char tmp;
    cin >> tmp;
    st += tmp;
  }
  cout << bfs(st) << endl;
  return 0;
}

acwing846

有向图

  • 邻接矩阵
  • 邻接表

DFS

通过idx标识每一条边，

h[a]获取该节点，然后通过ne[idx]访问对应关系，通过e[idx]访问下一节点

树的重心的性质：

还需理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010, M = N * 2;

int n;

int ans = N;

int h[N], e[M], ne[M],  idx;
//idx表示第n条边
//h[N] : 表示 第 i 个节点的 第一条边的 idx
//ne[M] : 表示 与 第 idx 条边 的 下一条边 的 idx
//e[M] : 表示 第idx 条边的 终点

bool st[N];	·//节点是否被访问过，访问过则标记为true

void add(int a,int b)
{
    e[idx] =  b;            //记录终点节点
    ne[idx] = h[a];        //相当于插入链表 ，将此节点后面的值传进来
    h[a] = idx ++;         //h[a]指向当前新增的节点
}

int dfs(int u)
{
    st[u] = true;
    int sum = 1, res = 0;
    for (int i = h[u]; i != -1; i = ne[i])		//从第一条边开始遍历
    {
        int j = e[i];		//下一条边
        if (!st[j])
        {
            int s = dfs(j);
            res = max (res, s);
            sum += s;

        }
    }
    res = max (res, n - sum);
    ans = min(ans, res);
    return sum;
}


int main()
{
    memset (h, -1, sizeof h);
    int a,b;
    cin >> n;
    for (int i = 0;i < n ; i ++)
        {
            cin >> a >>b;
            add(a, b), add(b, a);
        }

    dfs(1);
    cout << ans << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010, M = N * 2;

int n, m;


int h[N], e[M], ne[M], idx;
//idx表示第n条边

int d[N], q[N];
//q为队列，d为距离


void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++; 
}

int bfs(int u)
{
   int hh = 0, tt = 0;
   q[0] = 1;
   memset(d, -1, sizeof d);
    d[1] = 0;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; i != -1; i = ne[i])		
        {
            int j = e[i];
            if (d[j] == -1)
                {
                    d[j] = d[t] +1;
                    q[ ++ tt] = j;
                }


        }
    }
    return d[n];
}


int main()
{
    memset (h, -1, sizeof h);
 
    cin >> n >> m;
    for (int i = 0;i < m ; i ++)
        {
            int a,b;
            cin >> a >>b;
            add(a, b);
        }

    cout << bfs(1) << endl;
    return 0;
}

拓扑序列

  • 有向无环图
  • 一个有向无环图，一定至少有一个入度为0的点
  • 使用数组模拟队列可以输出路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010;

int n,m;

int h[N], e[N], ne[N], idx ;
int q[N], d[N];



void add(int a, int b)
{
    e[idx] = b;     
    ne[idx] = h[a];     
    h[a] = idx ++;
}

int topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++)
        if (!d[i])      //将入度为0的点入队
            q[ ++ tt] = i;
    
    while (hh <= tt)
    {
        int t = q[hh ++];

        for (int i = h[t]; i != -1; i = ne[i])  //bfs
        {
                int j = e[i];
                d[j] --;
                if (d[j] == 0)
                    q[++tt] = j;
        }
        
    }
    
    if(tt == n - 1){
        for(int i = 0; i < n; i++)
            cout << q[i] << " ";
        
    }
    else
            cout << -1;




}


int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >>b;
        d[b]++;
        add(a,b); 
    }

    topsort();
    return 0;


}

最短路

单源最短路
所有边权都为正数

  • 朴素Dijkstra算法O():稠密图

  • 堆优化版Dijkstra算法O(mlogn)：稀疏图

存在负权边

  • Bellman-Ford算法O(nm)

  • SPFA算法，一般O(m), 最坏O(nm)

多源汇点最短路

  • Floyd算法 O()

邻接矩阵

邻接表《链式前向星》

AcWing 849. Dijkstra求最短路 I

朴素Dijkstra算法

  1. 将除起点外的距离都置为无穷
  2. 选取当前点到另一未访问且距离最短的边
  3. 更新所有点到起点的距离
  4. 重复2——3，直到到达终点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 510;

int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N];  //用于记录该点的最短距离是否已经确定

int n, m;

int Dijkstra() {
  memset(dist, 0x3f, sizeof dist);
  dist[1] = 0;
  for (int i = 0; i < n; i++) //对每个点确定一次最短距离
  {
    int t = -1;
    for (int j = 1; j <= n; j++) {
      if (!st[j] && (t == -1 || dist[t] > dist[j]))     //选择没有访问且距离最短的下一点
        t = j;
    }
    st[t] = true;       //设置为已访问

    for (int j = 1; j <= n; j++) {
      dist[j] = min(dist[j], dist[t] + g[t][j]);   //更新与t有关点的最短距离
    }
  }

  if (dist[n] == 0x3f3f3f3f)
    return -1; //如果第n个点路径为无穷大即不存在最低路径
  return dist[n];
}

int main() {
  cin >> n >> m;
  memset(g, 0x3f, sizeof g);

  while (m--) {
    int a, b, c;
    cin >> a >> b >> c;
    //自环不会影响Dijkstra
    g[a][b] = min(g[a][b], c);  //重边的话选择最短边
  }
  cout << Dijkstra() << endl;
  return 0;
}

AcWing 850. Dijkstra求最短路 II

AcWing 850. 朴素Dijkstra与堆优化Dijkstra总结 - AcWing

使用优先队列模拟堆来实现距离的排序，同时再出队时遍历从该点出发的边实现更新最短距离值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 150010;

// 稀疏图用邻接表来存
int h[N], e[N], ne[N], idx;
int w[N]; // 用来存权重
int dist[N];
bool st[N];

int n, m;

void add(int a, int b, int c) {
  e[idx] = b;     //存终点
  ne[idx] = h[a]; //存上一条边索引
  w[idx] = c;     //存权重
  h[a] = idx++;   //存下标
}

int dijkstra() {
  memset(dist, 0x3f, sizeof dist);
  dist[1] = 0;
  priority_queue<PII, vector<PII>, greater<PII>> heap;
  heap.push({0, 1}); // 0表示距离，1表示节点,且位置不能变，因为优先队列排序方式
  while (heap.size()) {
    auto t = heap.top();
    heap.pop();
    int distance = t.first, node = t.second;

    if (st[node])
      continue; // 如果节点被访问过，则跳过
    st[node] = true;

    for (int i = h[node]; i != -1; i = ne[i]) { //遍历从该节点出发，所有边
      int j = e[i];
      if (dist[j] > dist[node] + w[i]) {
        dist[j] = dist[node] + w[i];
        heap.push({dist[j], j});
      }
    }
  }
  if (dist[n] == 0x3f3f3f3f)
    return -1;
  else
    return dist[n];
}

int main() {
  memset(h, -1, sizeof(h));
  scanf("%d%d", &n, &m);

  while (m--) {
    int x, y, c;
    scanf("%d%d%d", &x, &y, &c);
    add(x, y, c);
  }

  cout << dijkstra() << endl;

  return 0;
}

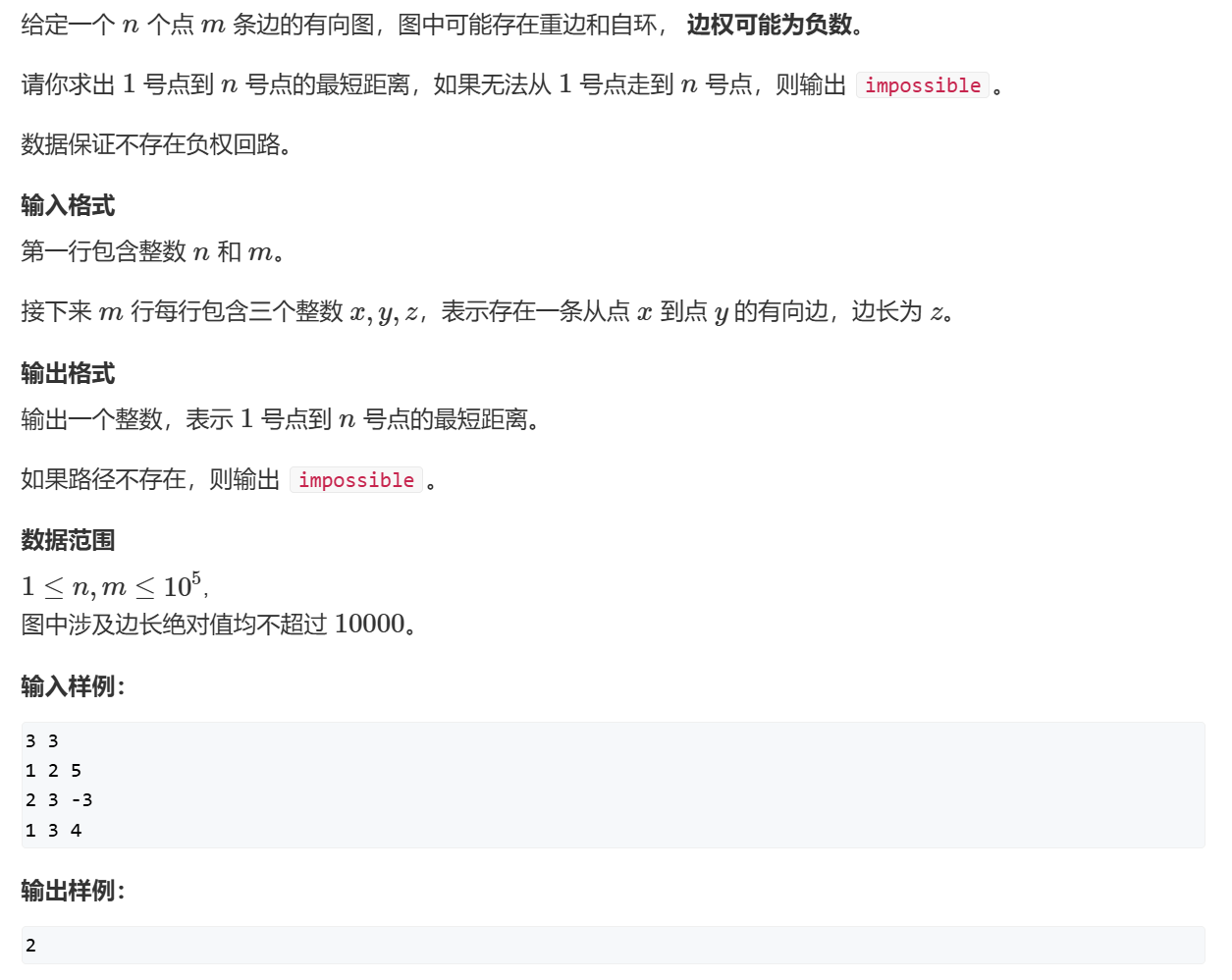
AcWing 853. 有边数限制的最短路

AcWing 853. 有边数限制的最短路 - AcWing解释了为什么Dijkstra不能使用在含负权的图中

Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge {
    int a;
    int b;
    int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边


void bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < k; i++)
    {
        memcpy(back, dist, sizeof dist);
        //对于每个点，都需要对每条边进行松弛操作
        //我们需要把每个点的最短距离保存下来，因为bellman_ford算法是迭代的，每次迭代都会更新最短距离
        for (int i = 0; i < m; i++) {
            int a = e[i].a, b = e[i].b, w = e[i].w;
            dist[b] = min(dist[b], back[a] + w);        //更新最短距离
        }
    }
}


int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    bellman_ford();
    //避免距离为-1的情况
    if(dist[n]>0x3f3f3f3f/2) //若最后一条边边权为负值，则距离可能小于0x3f3f3f3f
        puts("impossible");
    else printf("%d",dist[n]);

    return 0;
}

AcWing 851. spfa求最短路

AcWing 851. SPFA算法 - AcWing包含了算法的比较

SPFA算法和BFS算法差不多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];     // st数组的作用：判断当前的点是否已经加入到队列当中了



void add(int a, int b, int c){
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx++;
}


int spfa(){
    memset(dist, 0x3f, sizeof dist);
    queue<int> q;
    q.push(1);
    dist[1] = 0;
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;      //出队操作
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])  ///当前已经加入队列的结点，无需再次加入队列
                    {
                        st[j] = true;
                        q.push(j);
                    }
            }
        }
    }
    return dist[n];
}



int main(){
    memset(h, -1, sizeof h);
    memset(dist, 0x3f, sizeof dist);
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < m; i++){
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
    }
    spfa();
    if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷，则不能到达,因为spfa只遍历相连的边，而Bellman_ford遍历所有边 
        cout << "impossible";
    else cout << dist[n];
    return 0;
}

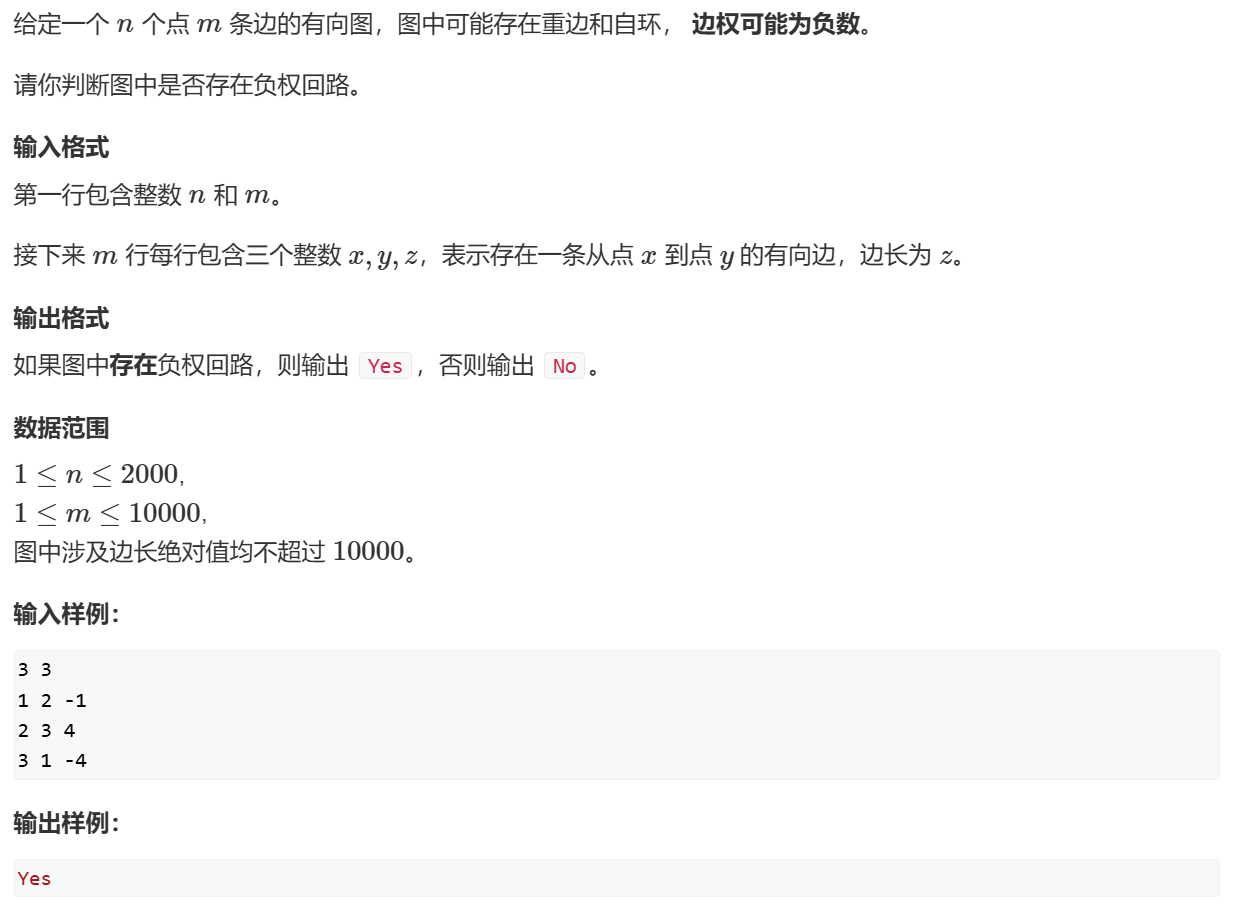
AcWing 852. spfa判断负环

AcWing 852. spfa判断负环 - AcWing

统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

const int N = 2e3 + 10, M = 1e4 + 10;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
bool st[N];
int dist[N];
int cnt[N]; // cnt[x] 表示 当前从1-x的最短路的边数

void add(int a, int b, int c) {
  e[idx] = b;
  ne[idx] = h[a];
  w[idx] = c;
  h[a] = idx++;
}

bool spfa() {
    //不用初始化dist，因为我们计算的是是否存在负环，根据的是节点数
  queue<int> q;
  for (int i = 1; i <= n; i++) {    //所有节点入队，因为可能是非连通图
    q.push(i);
    st[i] = true;
  }
  while (q.size()) {
    int t = q.front();
    q.pop();
    st[t] = false;

    for (int i = h[t]; i != -1; i = ne[i]) {
      int j = e[i];
      if (dist[j] > dist[t] + w[i]) {
        dist[j] = dist[t] + w[i];
        cnt[j] = cnt[t] + 1;
        // 如果边数超过节点数，说明存在负环
        if (cnt[j] >= n)
          return true;
         // 如果节点 j 不在队列中，则将其入队
        if (!st[j]) {
          q.push(j);
          st[j] = true;
        }
      }
    }
  }

  return false;
}

int main() {
  memset(h, -1, sizeof h);
  cin >> n >> m;
  for (int i = 0; i < m; i++) {
    int a, b, w;
    cin >> a >> b >> w;
    add(a, b, w);
  }
  if (spfa())
    cout << "Yes";
  else
    cout << "No";
  return 0;
}

最小生成树

  • 普利姆算法（Prim）
    • 朴素版Prim O(n^2) 稠密图
    • 堆优化版Prim O(mlogn)
  • 克鲁斯卡尔算法（Kruskal） O(mlogm) 稀疏图

二分图

  • 染色法 O(n+m)
  • 匈牙利算法 O(mn)，实际运行时间很小

AcWing858. Prim算法求最小生成树

Prem算法：我们从其中一个点出发，遍历该点所有边，找到最小权值的边，然后加入集合，更新该边另一顶点引出的边（使从该边引出的节点可达）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N];
bool st[N]; // 记录每个节点是否已经被包含在最小生成树中


int prim()
{
    memset(dist, 0x3f, sizeof dist);
    int res = 0;
    for(int i = 0; i < n; i ++ )
    {
        int t = -1;
        for(int j = 1; j <= n; j ++ )
            if(!st[j] && (t == -1 || dist[t] > dist[j]))    //贪心，找到距离当前集合的最小便
                t = j;
        if(i && dist[t] == INF) return INF;  //点不可达，不能生成最小树


        // 更新必须放在for循环前,避免自环，且当t放入集合后，其dist[t]已经没有意义
        if(i)   res += dist[t]; // 如果不是第一个点，将其权值加入结果中    
        st[t] = true;    

        for(int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]);        // 更新 dist 数组，记录每个节点到当前生成树的最小距离
        //即将一些点变为可达的点
    }
    return res;
}


int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);    //取最短边，Prim算法针对无向图，因此赋值两次
    }

    int t = prim();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

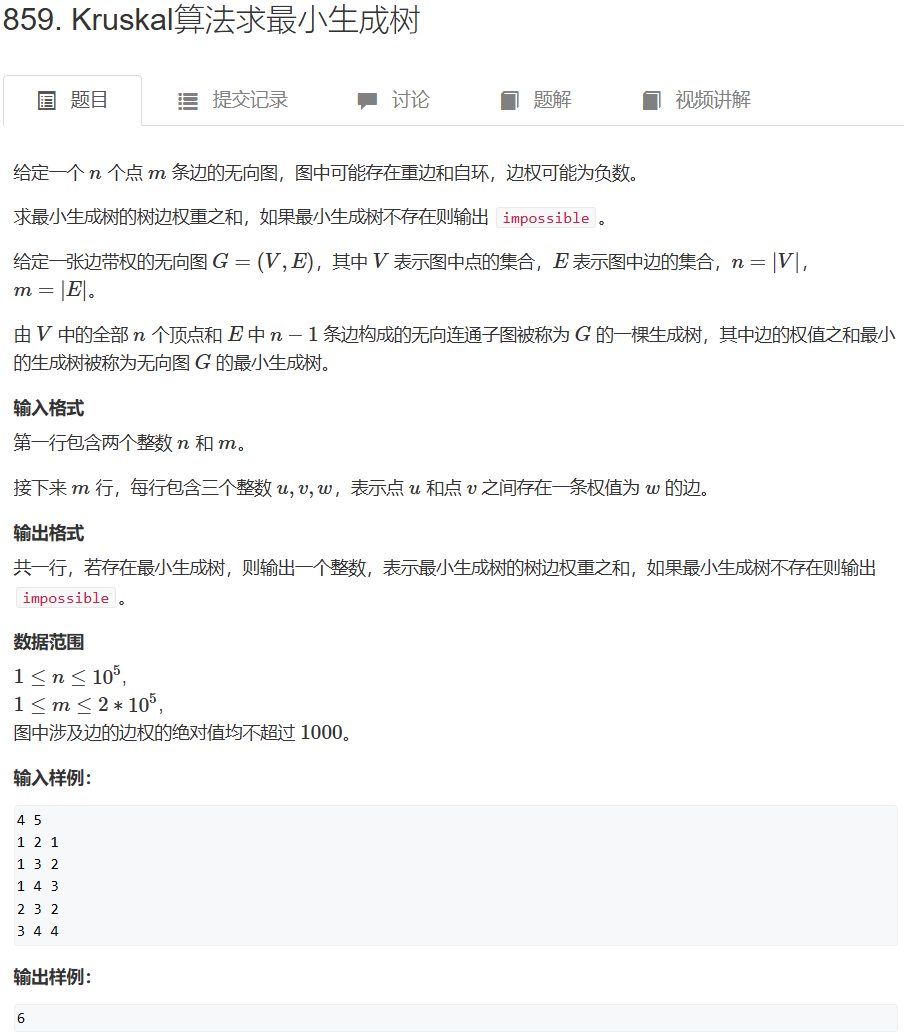
AcWing 859. Kruskal算法求最小生成树

kruskal算法：

通过并查集对边进行合并。先按照从小到大的权重进行排序，然后对每两个未连接的节点进行连边。我们知道，对于一个无向图，每两点有且仅有一条边相连，若其边数小于n-1，则其不联通，不能构成最小生成树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <cstring>
#include <algorithm>

using  namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge {
    int a, b, w;
    bool operator<(const Edge &E) const{
        return w < E.w;
    }
} edges[M];



int find(int x){        //并查集
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal(){
    sort(edges, edges + m);     
    for (int i = 1; i <= n; i ++ ) p[i] = i;    //初始化并查集
    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        if (a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }
    if (cnt < n - 1) return INF;        // 如果边的数量不足 n-1，说明图不连通
    else return res;
}



int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

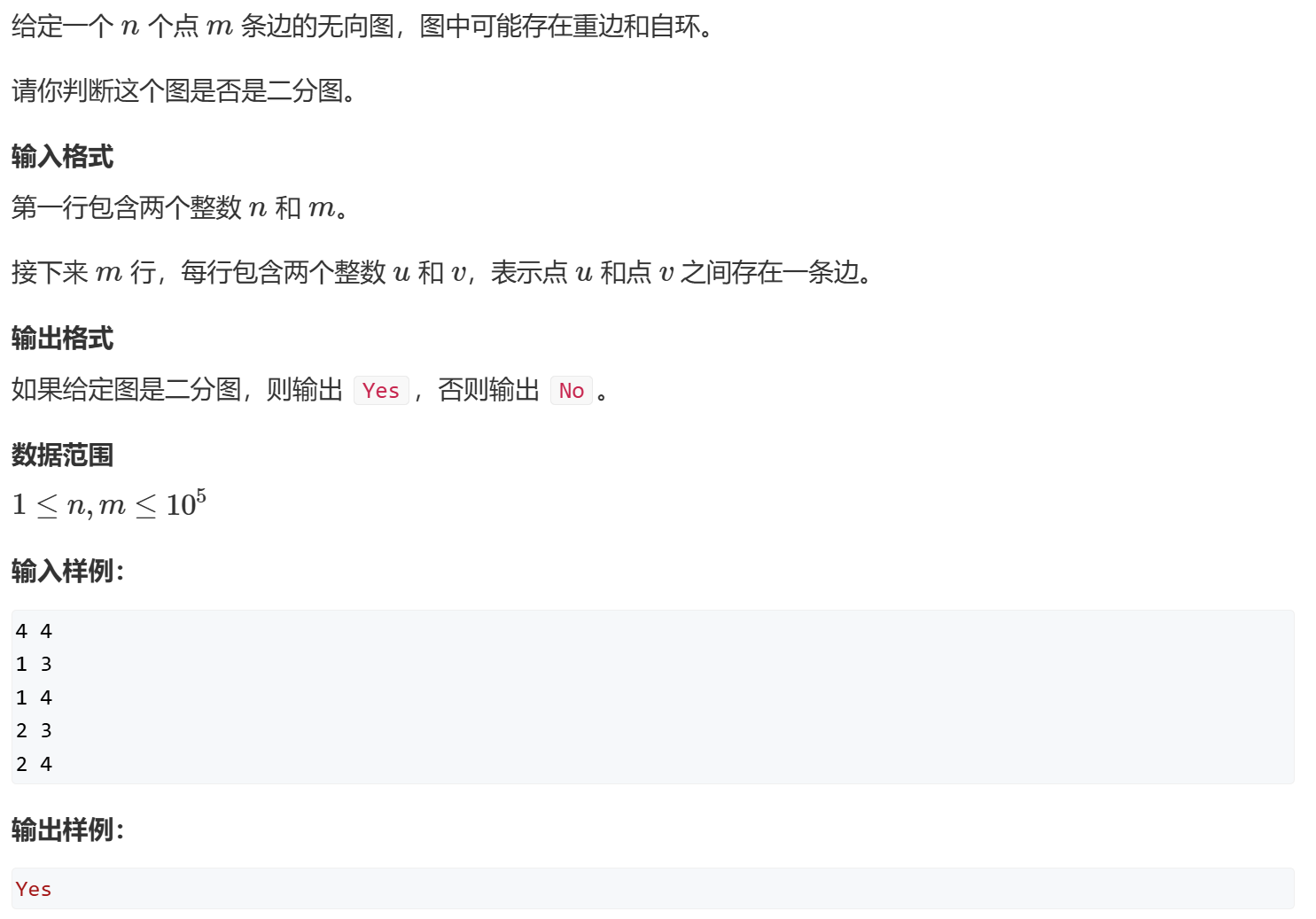
AcWing 860. 染色法判定二分图

  • 二分图：二分图是一种特殊的图，其顶点集可以分成两个互不相交的子集，使得每一条边的两个端点分别属于不同的子集。
  • 二部：如果一个图是二分图，那么它没有奇数长度的环。
  • 着色：一个图是二分图当且仅当它可以被 2-着色，即可以使用两种颜色对图的顶点进行着色，使得每条边的两个端点的颜色不同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010 * 2;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int color[N];//保存各个点的颜色，0 未染色，1 是红色，2 是黑色
int n, m;//点和边

void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool dfs(int u, int c)
{
    color[u] = c;//u的点成 c 染色

    for(int i = h[u]; i!= -1; i = ne[i])
    {
        int b = e[i];                   
        if(!color[b])
        {
            if(!dfs(b, 3 - c)) return false;//（3 - 1 = 2， 如果 u 的颜色是2，则和 u 相邻的染成 1）
                                            //（3 - 2 = 1， 如果 u 的颜色是1，则和 u 相邻的染成 2）
        }
        else if(color[b] && color[b] != 3 - c)//如果已经染色，判断颜色是否为 3 - c
        {                                     
            return false;              
        }
    }
    return true;
}



int main(){
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i = 0;i < m; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }
     for(int i = 1; i <= n; i++)//遍历点
    {
        if(!color[i])//如果没染色
        {
            if(!dfs(i, 1))//染色该点，并递归处理和它相邻的点
            {
                cout << "No" << endl;
                return 0;
            }

        }
    }
    cout << "Yes" << endl;
    return 0;

}

AcWing 861. 二分图的最大匹配

匈牙利算法：

匈牙利算法是一种用于解决指派问题（Assignment Problem）的数学算法。指派问题是指在有限的候选者中选择一组匹配，使得总的成本最小（或收益最大）。

find(int u): 尝试为左边节点 u 找到一个匹配，使用递归方式实现深度优先搜索（DFS）。

如果右边节点 j 未被访问过，则标记为已访问。

如果右边节点 j 未匹配或者其匹配的左边节点可以重新匹配，则更新匹配关系并返回 true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstring>
using namespace std;

const int N = 505, M = 1e5 + 10;

int n1,n2, m;
int h[N], e[M], ne[M], idx;

int match[N], st[N];


void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int find(int u) // 匈牙利算法
{
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            st[j] = true;      //标记该节被占用，后续调用不能使用该节点
            if(match[j] == 0 || find(match[j])){    //如果该节点没有被匹配，则匹配
                                                    //若该节点已匹配，则递归调用重新匹配节点
                match[j] = u;
                return true;
            }
        }
    }
    return false;
}

int main(){
    memset(h, -1, sizeof h);
    scanf("%d%d%d", &n1, &n2, &m);
    for(int i = 0; i < m; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
     int res = 0;
    //为各个点找匹配
    for(int i = 1; i <= n1; i++){
        memset(st, 0, sizeof st);   //将st数组置0，使得所有节点都没有被标记
        if(find(i)) res++;
    }
    cout << res;
    return 0;
}