贪心

TODO：畜栏预定、雷达设备

区间问题

贪心题的要点：

  • 思考、证明通过该方法得到的解是最优解。

  • 证明：res <= ans，res >= ans ——> res == ans。

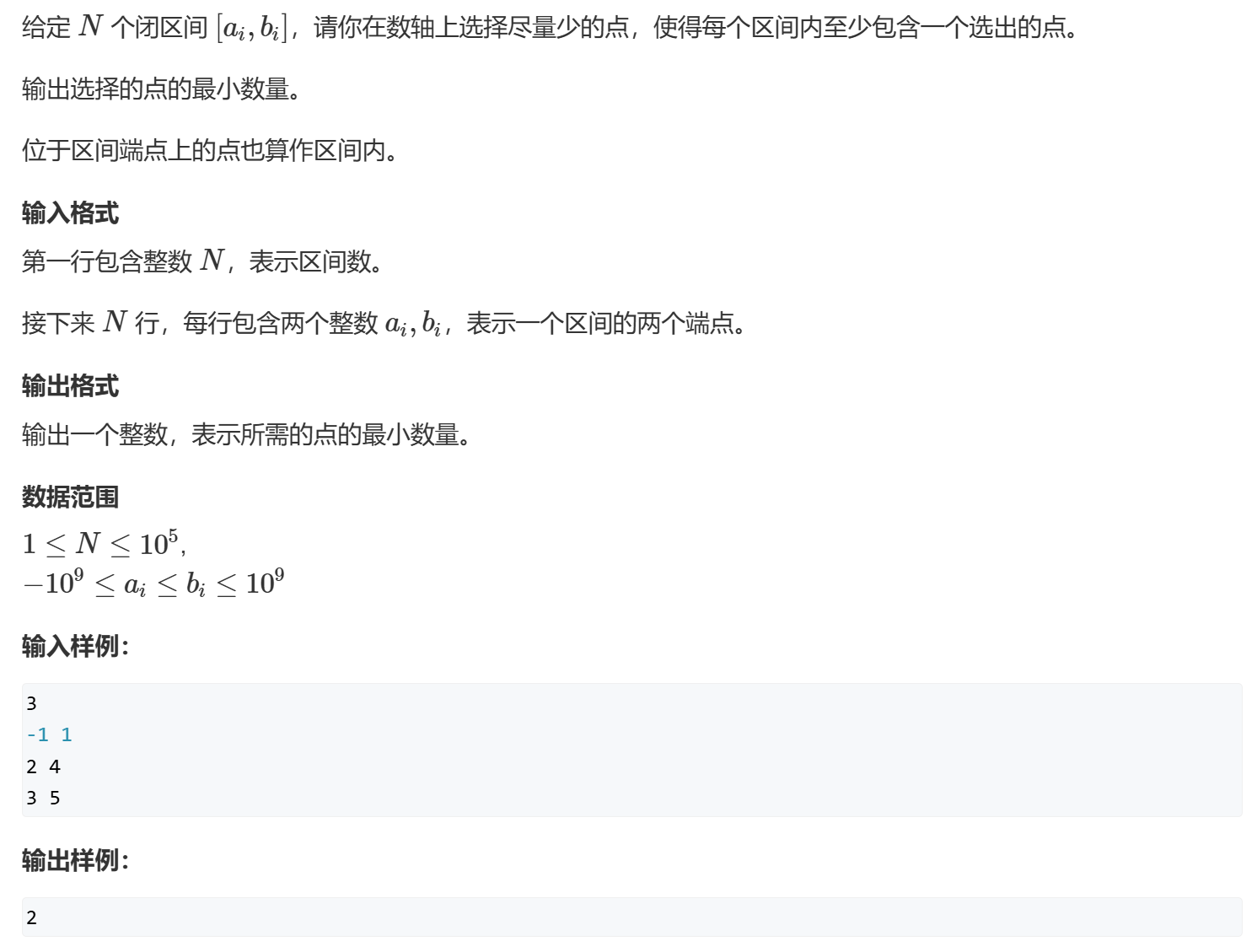
acwing905

我们通过重载运算符，设置为通过右端点从小到大排序，获取第一个右端点最大值为max值，若其他线段的左端点小于该max值，则continue。若大于则更新max值，res++。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <algorithm>
#include <iostream>

using namespace std;
const int N = 100010;

struct st {
  int lef;
  int rig;
  bool operator<(const st &tmp) const { return this->rig < tmp.rig; }
} st[N];

int main() {
  int n;
  cin >> n;     //别忘了输入n Qwq
  for (int i = 0; i < n; i++) {
    cin >> st[i].lef >> st[i].rig;
  }
  sort(st, st + n);
 
  int max = -2e9;
  int res = 0;
  for (int i = 0; i < n; i++) {
    if (st[i].lef > max) {
      max = st[i].rig;
      res++;
    }
  }
  cout << res << endl;
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from functools import cmp_to_key

class point:
    def __init__(self,a,b):
        self.a =  a
        self.b =  b

def cmp(x, y):
    if x.b != y.b:
        return x.b - y.b  # 按右端点升序排序
    return x.a - y.a      # 右端点相同则按左端点升序

n = int(input())

points = []

for i in range(n):
    a,b = map(int,input().split())
    points.append(point(a,b))

points.sort(key=cmp_to_key(cmp))

cnt = 0
right = -1e9-10
for i in range(n):
    if points[i].a > right:
        cnt += 1
        right = points[i].b
        
print(cnt)

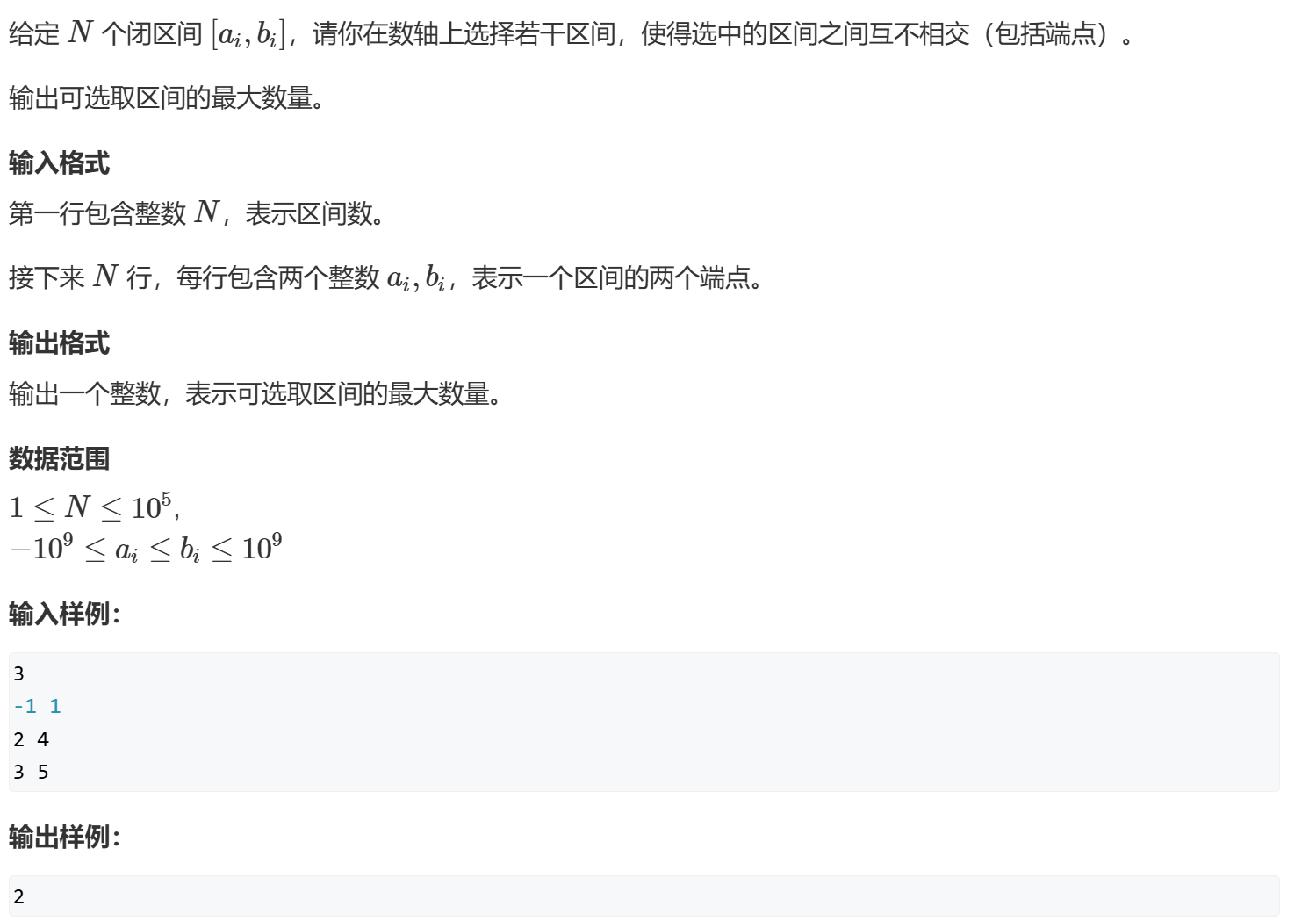
acwing908

这题可以采用右端点排序，也可以采用左端点排序。

cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

const int N = 1e5 + 5;


struct st{
    int lef;
    int rig;
    bool operator< (const st& tmp)  const{
        return this->rig < tmp.rig;
    }
}st[N];


int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> st[i].lef >> st[i].rig; 
    }
    sort(st,st + n);
    int res = 0;
    int rigmax  = -2e9;
    for(int i = 0; i < n; i ++)
    {
        if(st[i].lef > rigmax)
        {
            rigmax = st[i].rig;
            res ++;
         }
    }
    cout << res << endl;
    
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from functools import cmp_to_key


class point:
    def __init__(self,a,b):
        self.a =  a
        self.b =  b


def cmp(x, y):
    if x.b != y.b:
        return x.b - y.b  # 按右端点升序
    return y.a - x.a      # 右端点相同则按左端点降序
    
points = []
    
n = int(input())

for i in range(n): 
    a,b = map(int,input().split())
    points.append(point(a,b))
    
    
points.sort(key=cmp_to_key(cmp))

righ = -1e9-10
cnt = 0
for i in range(n):
    if points[i].a > righ:
        cnt += 1
        righ = points[i].b

print(cnt)

区间选点问题和最大不相交区间数量的区别

  1. 按右端点排序保证贪心最优性
  2. 跨过当前右端点的区间都会被后续的点覆盖
  3. 计数逻辑在数学上完全等价

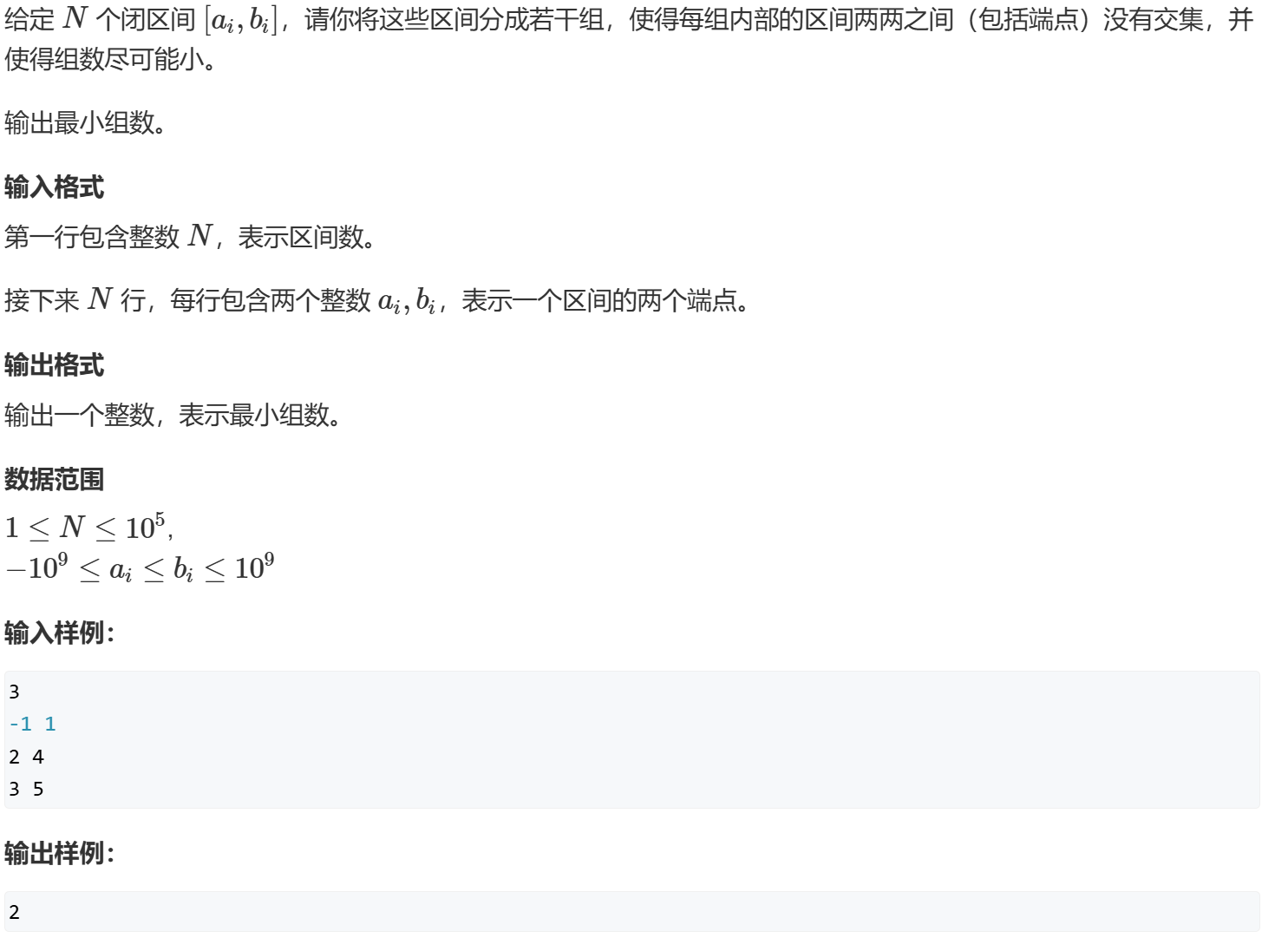
acwing906

python
贪心
  • 按左端点排序，保证正向遍历时区间是稠密的
  • 我们通过优先队列模拟小根堆，小根堆堆顶维护当前组右端点的最小值（若最小值都无法插入，则其他组也无法插入该区间）
    • 能插入，更新堆顶为当前区间右端点
    • 不能插入，插入当前区间右端点
    • 此时堆重新排序，产生新的右端点最小值
  • 为什么不能为大根堆：
    • 小根堆：保证每次选择最小的右端点，覆盖尽可能多的区间，得到最少点数。等价于选择最早结束的区间。
    • 大根堆：会错过更优的覆盖机会，导致点数增加。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from queue import PriorityQueue
from functools import cmp_to_key    

n = int(input())

class Node:
    def __init__(self,a,b):
        self.a = a
        self.b = b

class lefnode:
    def __init__(self,p):
        self.p = p
    def __lt__(self,other):
        return self.p < other.p

def cmp(x,y):
    return x.a - y.a


nodes = []


for i in range(n):
    a,b = map(int,input().split())
    nodes.append(Node(a,b))

nodes.sort(key=cmp_to_key(cmp))

# for i in range(n):
#     print(nodes[i].a,nodes[i].b)
    
q = PriorityQueue()

q.put(lefnode(-1e9-10))

for i in range(n):
    x = q.get()
    if q.empty() or x.p >= nodes[i].a:
        q.put(x)
        q.put(lefnode(nodes[i].b))
    else:
        q.put(lefnode(nodes[i].b))
    
# for i in range(n):
#     q.put(nodes[i])
    
print(q.qsize())
差分

参考题解AcWing 906. 区间分组（200 +ms） - AcWing

这题也属于区间重叠问题，使用不用数组的差分思想（扫描线算法）

  • 将区间覆盖转化为”开始”和”结束”事件

  • 通过+1和-1表示覆盖变化

  • (a, 1)：表示在坐标 a 处有一个区间开始

  • (b+1, -1)：表示在坐标 b+1 处有一个区间结束
  • ans += b：根据事件类型调整当前重叠数
  • maxans = max(maxans, ans)：记录最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
n = int(input())

arr = []

for i in range(n):
    a,b = map(int,input().split())
    arr.append((a,1))		
    arr.append((b+1,-1))
    
arr.sort(reverse = False)


ans = 0
maxans = 0

for a,b in arr:
    ans += b
    maxans = max(maxans,ans)

print(maxans)

Huffman树

acwing148

哈夫曼编码（Huffman Coding）是一种贪心算法的应用，用于构造最优前缀码，实现数据的高效压缩。其核心思想是：频率越高的字符，分配的编码越短。

哈夫曼算法通过以下步骤实现贪心选择：

  1. 将字符按频率升序排序。
  2. 每次合并频率最小的两个节点，生成新节点（频率为两者之和）。
  3. 重复合并，直到只剩一个根节点。

贪心选择性质：每次合并当前最小的两个节点，保证局部最优导致全局最优。

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from queue import PriorityQueue
n = int(input())

heap = PriorityQueue()

arr = list(map(int,input().split()))


for i in arr:
    heap.put(i)
    
res = 0
    
while heap.qsize() > 1:
    a = heap.get()
    b = heap.get()
    res += a+b
    heap.put(a+b)
    
print(res)

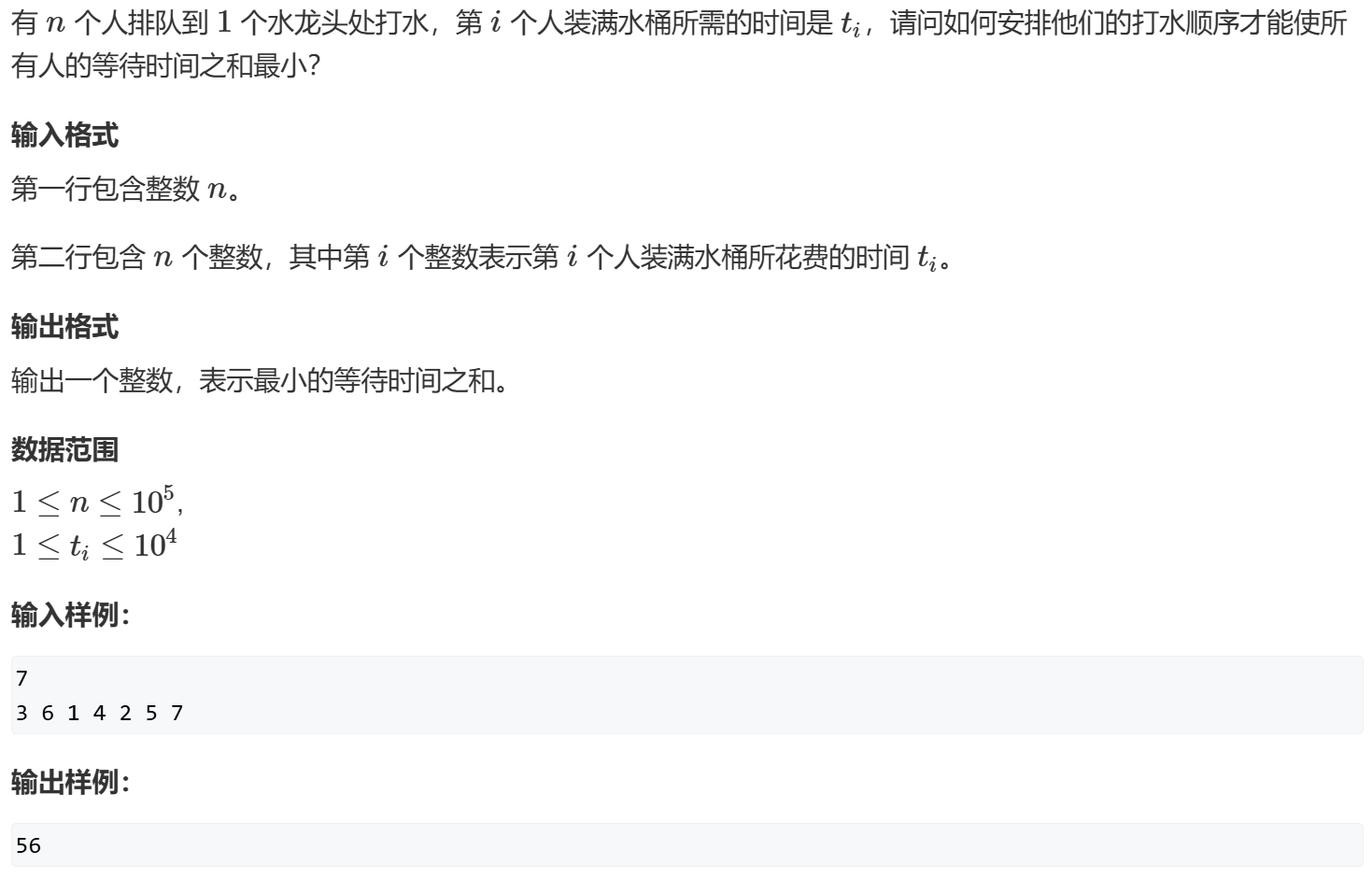
排序不等式

acwing913

1
2
3
4
5
6
7
n = int(input())
t = list(map(int, input().split()))
t.sort()  
total_time = 0
for i in range(n):
    total_time += t[i] * (n - i - 1)  # 第i个人的打水时间会被后面(n-i-1)个人等待
print(total_time)

AcWing 104. 货仓选址

1
2
3
4
5
6
7
8
n = int(input())
arr = list(map(int, input().split()))
arr.sort()

median = arr[n // 2]  # 中位数
total_distance = sum(abs(x - median) for x in arr)

print(total_distance)

对于两个