[toc]

acwing826. 单链表

头插法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <cstring>
using namespace std;

const int N = 100005;
int head, e[N], ne[N], idx; 
//头节点， 值，下一节点，idx索引节点的编号
void init()
{
    head = -1;
    idx = 0;
}

void add_to_head(int x  )
{
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx ++;
}

void remove(int pos)
{
    ne[pos] = ne[ne[pos]];
}


void insert(int x, int pos)
{
    e[idx] = x;
    ne[idx] = ne[pos];
    ne[pos] = idx;
    idx++;

}
int main()
{
    int m;
    cin >> m;

    init();

    while(m--)
    {
        char op;
        int pos, x;
        cin >> op;
        if(op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if(op == 'D')
        {
            cin >> pos;
            if(!pos) head = ne[head];   //移除头节点
            else remove(pos - 1);//第k个元素对应的索引为k - 1
        }
        else 
        {
            cin >> pos >> x;
            insert(x, pos -1);//第k个元素对应的索引为k - 1
        }
    }
    for(int i = head; i != -1; i = ne[i]) cout << e[i] << " ";

    cout<< endl;
}


827.双链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>

using namespace std;

const int N = 1e5 + 5;

int l[N], r[N], e[N];
// l表示该节点左边，r表示该节点右边
int idx;

void init() {
  l[1] = 0;
  r[0] = 1;		// 第一个点的右边是 1   第二个点的左边是 0，这两个点都会随着链表变化
  idx = 2; //已经用掉两个节点
}

// k点右边插入x
void add(int k, int x) {
  e[idx] = x;
  r[idx] = r[k];
  l[idx] = k;
  l[r[idx]] = idx;
  r[k] = idx;
  idx++;
}

void remove(int k) {
  r[l[k]] = r[k];
  l[r[k]] = l[k];
}

int main() {
  int m;
  cin >> m;
  init();
  while (m--) {
    string op;
    cin >> op;
    int k, x;
    if (op == "R") {
      cin >> x;
      add(l[1], x); //指向最右边的节点
    } else if (op == "L") {
      cin >> x;
      add(0, x); //指向最左边的节点
    } else if (op == "D") {
      cin >> k;
      remove(k + 1);
    } else if (op == "IL") {
      cin >> k >> x;
      add(l[k + 1], x); // k点右边插入
    } else if (op == "IR") {
      cin >> k >> x;
      add(k + 1, x);
    }
  }
  for (int i = r[0]; i != 1; i = r[i])
    cout << e[i] << ' ';
  return 0;
}

828.模拟栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
using namespace std;
const int N = 100010;
int st[N];
int top = -1;
int n;


int main()
{
    cin >> n;
    while(n -- )
    {
        string s;
        cin >> s;
        if(s == "push")
        {
            cin >> st[++top];
        }
        if(s == "query")
        {
            cout << st[top] << endl;
        }
        if(s == "pop")
        {
            top--;
        }
        if(s == "empty")
        {
            if(top == -1)   cout << "YES" << endl;
            else            cout << "NO" << endl;
        }
    }
    return 0;
}

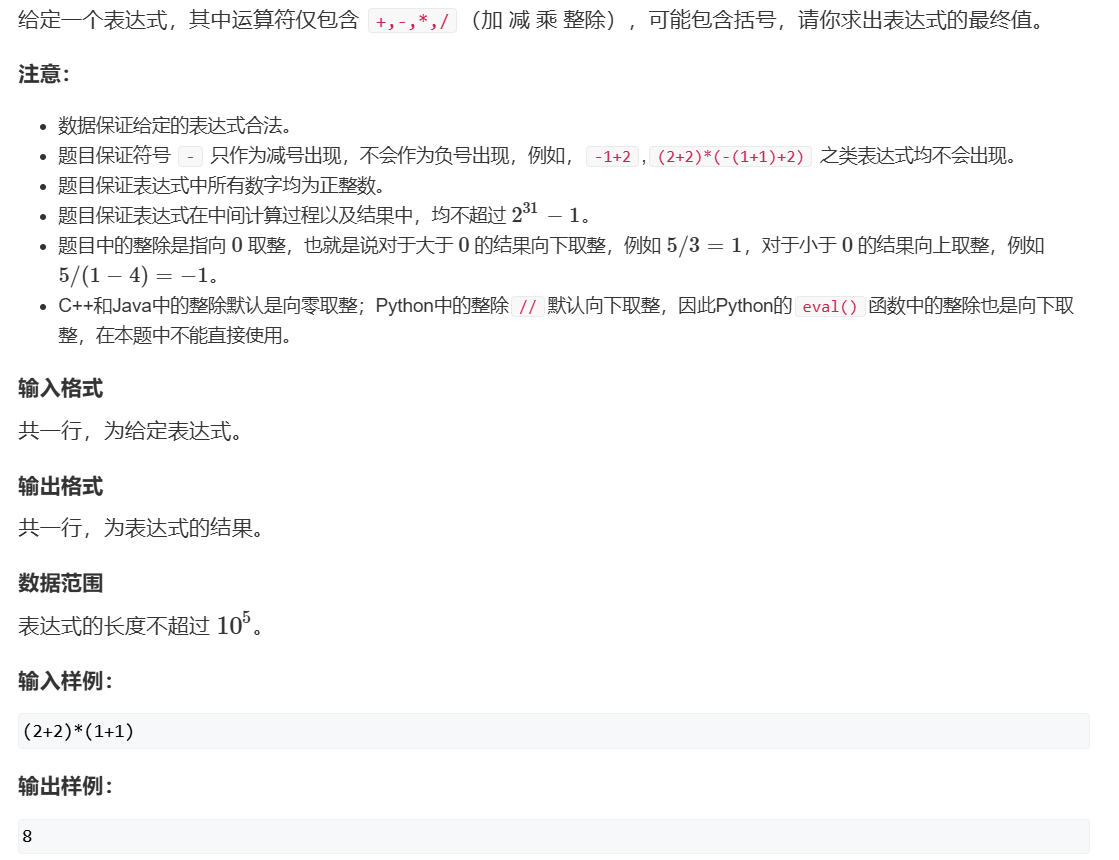
3302. 表达式求值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <stack>
#include <string>
#include <unordered_map>
using namespace std;

stack<int> num;
stack<char> op;

unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};

void eval() {
  int a = num.top();
  num.pop();
  int b = num.top();
  num.pop();
  char c = op.top();
  op.pop();
  int res = 0;
  if (c == '+')
    res = b + a;
  if (c == '-')
    res = b - a;
  if (c == '*')
    res = b * a;
  if (c == '/')
    res = b / a; //注意顺序

  num.push(res);
}

int main() {
  string s;
  cin >> s;
  int idx = 0;
  for (int i = 0; i < s.size(); i++) {
    if (isdigit(s[i])) {
      int j = i, res = 0;
      while (j < s.size() && isdigit(s[j])) {
        res = res * 10 + (s[j] - '0'); //可以不借助carry实现
        j++;
      }
      i = j - 1;
      num.push(res);
    } else if (s[i] == '(') {
      op.push('(');

    } else if (s[i] == ')') {
      while (op.top() != '(') {		//匹配到上一(
        eval();
      }
      op.pop(); //将'('出栈
    } else if (h.count(s[i])) {
      while (op.size() &&
             h[op.top()] >= h[s[i]]) //待入栈运算符优先级低，则先计算
        eval();                      //如 ***+ 的情况
      op.push(s[i]);                 //操作符入栈
    }
  }
  while (op.size())
    eval();                  //剩余的进行计算
  cout << num.top() << endl; //输出结果
  return 0;
}

829. 模拟队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>

using namespace std;

const int N = 100005;
int q[N];
int hh = 0;
int tt = -1;

int main() {
  int n;
  string s;
  cin >> n;
  while (n--) {
    cin >> s;
    if (s == "push") {
      cin >> q[++tt];
    }
    if (s == "pop") {
      hh++;
    }
    if (s == "query") {
      cout << q[hh] << endl;
    }
    if (s == "empty") {
      if (hh > tt)
        cout << "YES" << endl;
      else
        cout << "NO" << endl;
    }
  }
}

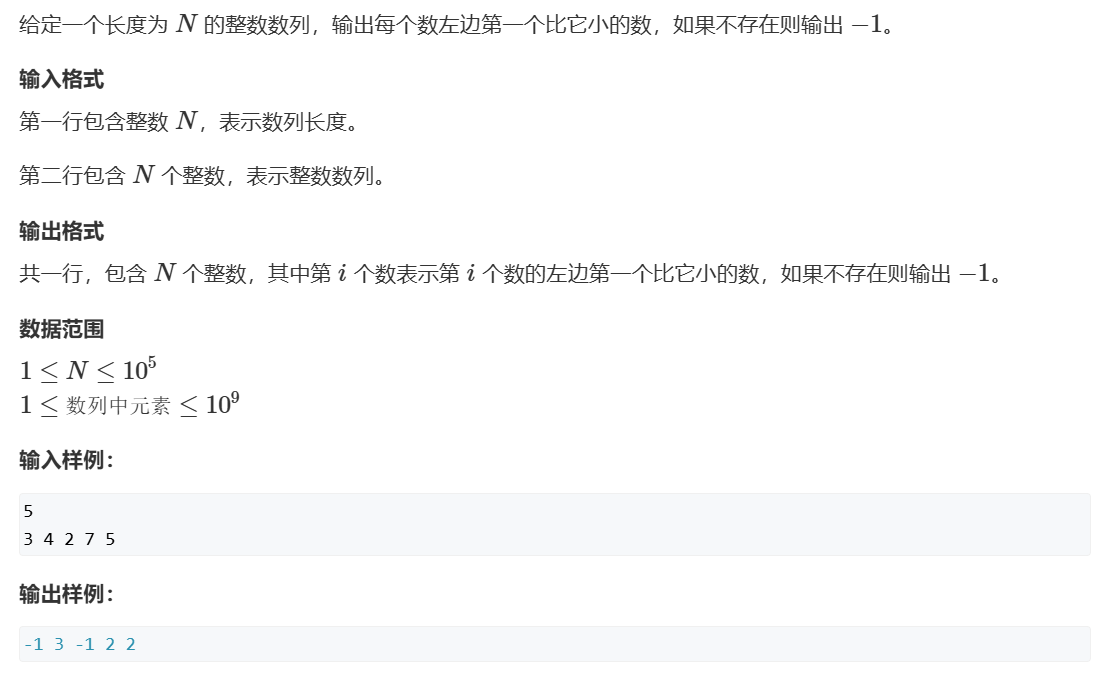
830. 单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <stack>

using namespace std;

stack<int> st;

int main() {
  int n, tmp;
  cin >> n;
  st.push(-1);
  while (n--) {
    cin >> tmp;

    while (tmp <= st.top())

      st.pop();

    cout << st.top() << " ";

    st.push(tmp);
  }
}

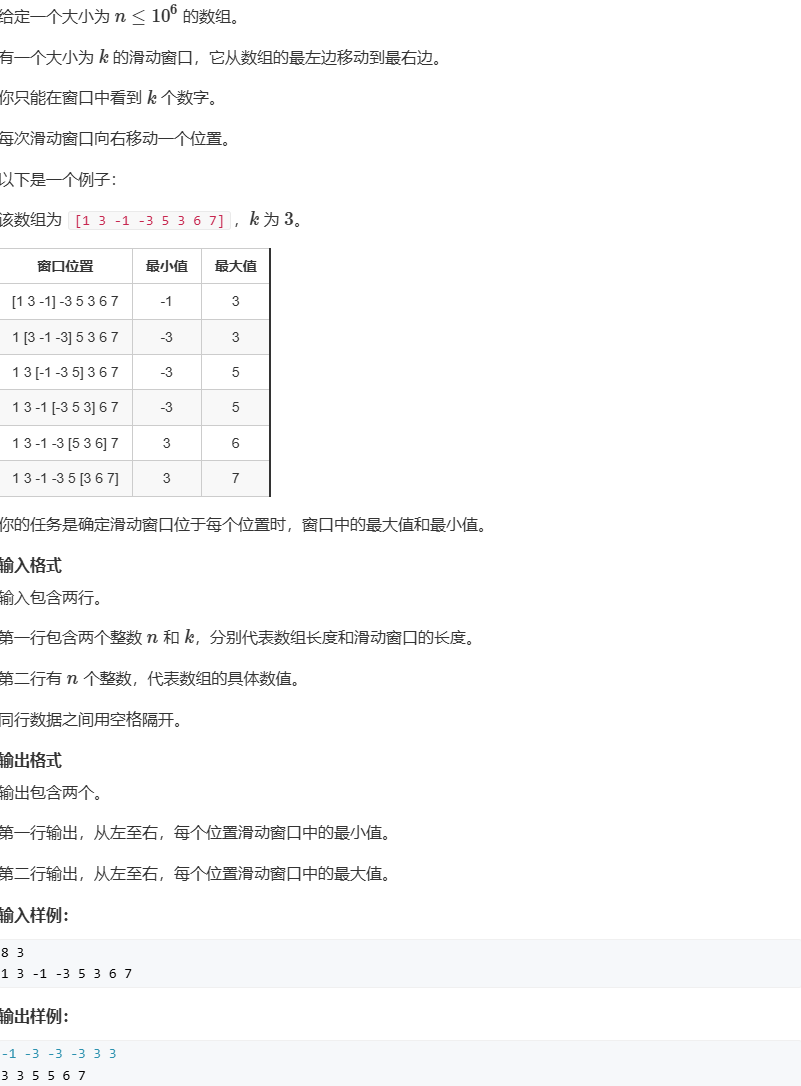
154 滑动窗口

通过在队头维持当前窗口的最小值来实现滑动窗口。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
using namespace std;

const int N = 1000010;
int a[N];
int main()
{
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];//读入数据
    deque<int> q;
    for(int i = 1; i <= n; i++)
    {
        while(q.size() && q.back() > a[i]) //新进入窗口的值小于队尾元素，则队尾出队列
            q.pop_back();
        q.push_back(a[i]);//将新进入的元素入队
        if(i - k >= 1 && q.front() == a[i - k])//若队头是否滑出了窗口，队头出队 
            q.pop_front();
        if(i >= k)//当窗口形成，输出队头对应的值
            cout << q.front() <<" ";
    }
    q.clear();
    cout << endl;

    //最大值亦然
    for(int i = 1; i <= n; i++)
    {
        while(q.size() && q.back() < a[i]) q.pop_back();
        q.push_back(a[i]);
        if(i - k >= 1 && a[i - k] == q.front()) q.pop_front(); 
        if(i >= k) cout << q.front() << " ";

    }
}

831. KMP字符串

感觉这个记了没半小时就忘了ಥ_ಥ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>

using namespace std;

const int N = 100010, M = 1000010;

int n, m;
int ne[N];
char s[M], p[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;

    for (int i = 2, j = 0; i <= n; i ++ )
    {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

    for (int i = 1, j = 0; i <= m; i ++ )
    {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == n)
        {
            printf("%d ", i - n);
            j = ne[j];
        }
    }

    return 0;
}

Trie树(前缀树或字典树)

高效存储查找字符串

835. Trie字符串统计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>

using namespace std;

const int N = 100010;
//son[][]存储子节点的位置，分支最多26条；
//cnt[]存储以某节点结尾的字符串个数（同时也起标记作用）
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][32], cnt[N], idx;
char str[N];



void insert(char * str){
    int p = 0;		//节点1
    for(int i = 0; str[i]; i++){
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];		//移动到子节点  
    }
    cnt[p]++;			//以某节点结尾的字符串个数
}


int query(char *str){
    int p = 0;
    for(int i = 0; str[i]; i++){
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
 }


int main()
{
    int m;
    cin >> m;

    while(m--)
    {
        char op[2];
        scanf("%s%s", op, str);

        if(*op == 'I') insert(str);
        else printf("%d\n", query(str));
    }

    return 0;
}

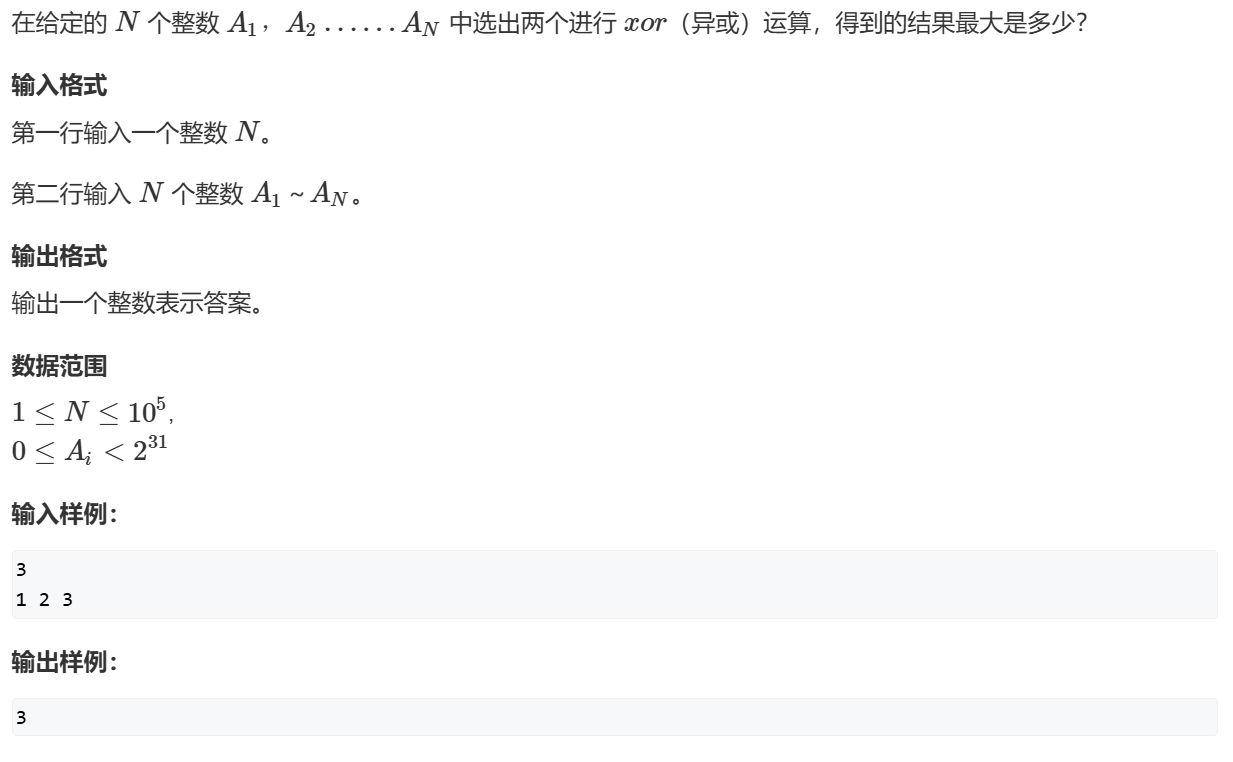
143. 最大异或对

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int son[N*31][2], idx,n,a[N];

void insert(int x)
{
  int p = 0;
  for (int i = 30; i >= 0; i--)		//右移30才是第一位
  {
    int u = x >> i & 1;
    if (!son[p][u])
      son[p][u] = ++idx;
    p = son[p][u];
  }
}

int  query(int x)	//前x位相同的异或值
{
  int p = 0,res = 0;
  for (int i = 30; i >= 0; i--)
  {
    int u = x >> i & 1;
    if (son[p][!u])	
    {
      p = son[p][!u];
      res = res * 2 + 1;
    }
    else
    {
      p = son[p][u];
      res = res * 2+0;
    }
  }
  return res;
}
int main()
{
  cin >> n;
  for (int i = 0; i < n; i++)
  {
    cin >> a[i];
    insert(a[i]);
  }
  int res = 0;
  for (int i = 0; i < n; i++)
  {
    res = max(res, query(a[i]));
  }
  cout << res;

  return 0;
}

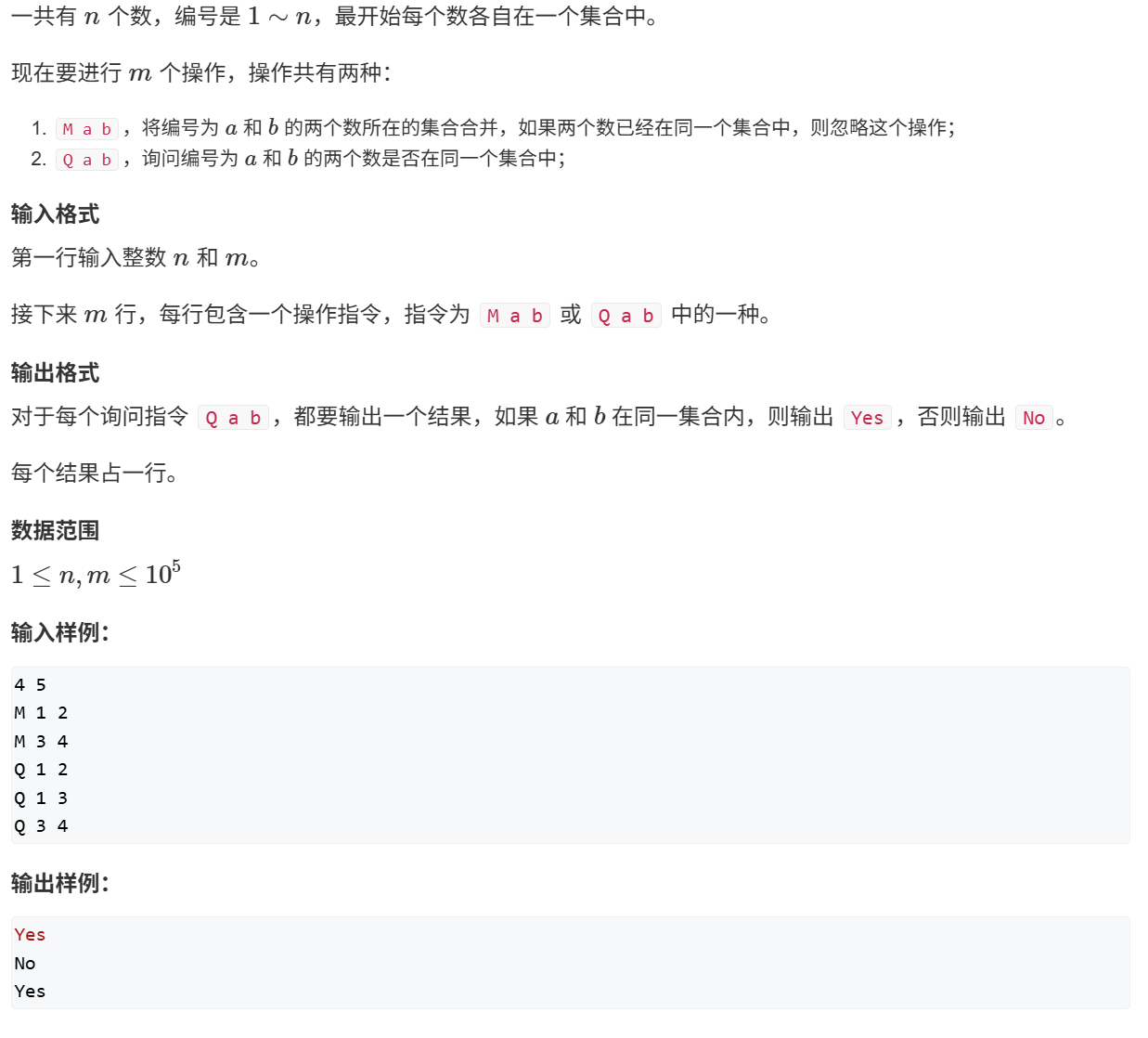
并查集

  • 将含有两个元素的两个集合合并
  • 询问两个元素是否在一个集合中

优化：路径压缩

1
2
3
4
5
6
7
int find(int x) {
  if (p[x] != x)
    p[x] =find(p[x]);		//路径压缩
  return p[x];		//返回头节点
}
 for (int i = 1; i <= n; i++)
    p[i] = i;			//初始化并查集

acwing 836. 合并集合

cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>

const int N = 100050;
int n, m;
int p[N];

int find(int x) {
  if (p[x] != x)
    p[x] =find(p[x]);		//路径压缩
  return p[x];		//返回头节点
}

int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++)
    p[i] = i;			//将每个元素放入一个堆

  while (m--) {
    char op[2];
    int a, b;
    scanf("%s%d%d", op, &a, &b);
    if (op[0] == 'M')
      p[find(a)] = find(b);		//将a的头节点插入b
    else {
      if (find(a) == find(b))
        puts("Yes");
      else
        puts("No");
    }
  }
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import sys
input = lambda: sys.stdin.readline().strip()

n, m = map(int, input().split())

# 初始化
p = [i for i in range(n+1)]
size = [1] * (n+1)  # 按秩合并

# 非递归find
def find(x):
    while p[x] != x:
        p[x] = p[p[x]]  # 路径压缩
        x = p[x]
    return p[x]

for _ in range(m):
    op, *args = input().split()
    if op == "Q":
        a, b = map(int, args)
        print("Yes" if find(a) == find(b) else "No")
    elif op == "M":
        a, b = map(int, args)
        root_a = find(a)
        root_b = find(b)
        if root_a != root_b:
            if size[root_a] > size[root_b]:
                p[root_b] = root_a
                size[root_a] += size[root_b]
            else:
                p[root_a] = root_b
                size[root_b] += size[root_a]

837. 连通块中点的数量

我们只需要再维持一个点的数量的数组。

cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
using namespace std;

const int N = 1000050;

int n, m;


int p[N], siz[N];


int find(int x){
    if(p[x] != x)   p[x] = find(p[x]);
    return p[x];    //p[x]已经被更新
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)  
    {
        p[i] = i;
        siz[i] = 1;
    }
    while(m--)

    {
        char op[5];
        scanf("%s", op);
        int a, b;
        if(op[0] == 'C')
        {
            scanf("%d%d", &a, &b);
            if(find(a) == find(b)) continue;	//同一连通图内点相连直接continue
            siz[find(b)] += siz[find(a)];
            p[find(a)] = find(b);
        }   
        else if(op[1] == '2')
        {
            scanf("%d", &a);
            printf("%d\n", siz[find(a)]);
        }
        else
        {
            scanf("%d%d", &a, &b);
            if(find(a) == find(b))  puts("Yes");
            else puts("No");
        }


    }


}

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import sys
sys.setrecursionlimit(100000)  
input = lambda: sys.stdin.readline().strip()

n, m = map(int, input().split())

p = [i for i in range(n+1)]  
siz = [1] * (n+1)            

def find(x):
    if p[x] != x:
        p[x] = find(p[x])
    return p[x]

for _ in range(m):
    parts = input().split()
    op = parts[0]
    
    if op == "C":
        a, b = map(int, parts[1:])
        root_a = find(a)
        root_b = find(b)
        if root_a != root_b:
            p[root_a] = root_b
            siz[root_b] += siz[root_a]
            
    elif op == "Q1":
        a, b = map(int, parts[1:])
        print("Yes" if find(a) == find(b) else "No")
        
    elif op == "Q2":
        a = int(parts[1])
        print(siz[find(a)])

240. 食物链

  • 余1可以吃根节点
  • 余2可以被根节点吃
  • 余3与根节点同类

//TODO

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
using namespace std;

const int N = 5 * 1e4 + 10; // 定义最大节点数
int n, m; // n表示节点数，m表示操作数
int p[N], d[N]; // p数组存储每个节点的父节点，d数组存储每个节点到其父节点的距离

// 查找函数，带路径压缩和距离更新
int find(int x) {
    if (p[x] != x) {
        int t = find(p[x]); // t暂时存储x的父节点的根节点
        d[x] += d[p[x]]; // 更新x到根节点的距离
        p[x] = t; // 路径压缩
    }
    return p[x]; // 返回根节点
}

int main() {
    cin >> n >> m;
    // 初始化，每个节点的父节点为其自身
    for (int i = 1; i <= n; i++) {
        p[i] = i;
    }
    int res = 0; // 记录不合法操作的次数

    while (m--) {
        int r, x, y;
        cin >> r >> x >> y;

        // 检查输入是否合法
        if (x > n || y > n) {
            res++;
        } else {
            int px = find(x), py = find(y);

            // 处理r == 1的情况
            if (r == 1) {
                // 如果x和y在同一个集合中且不满足距离关系，则计数加1
                if (px == py && (d[x] - d[y]) % 3) {
                    res++;
                } else if (px != py) {
                    // 合并两个集合，更新距离关系
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            // 处理r == 2的情况
            else if (r == 2) {
                // 如果x和y在同一个集合中且不满足距离关系，则计数加1
                if (px == py && (d[x] - d[y] - 1) % 3) {
                    res++;
                } else if (px != py) {
                    // 合并两个集合，更新距离关系
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    cout << res; // 输出不合法操作的次数
}

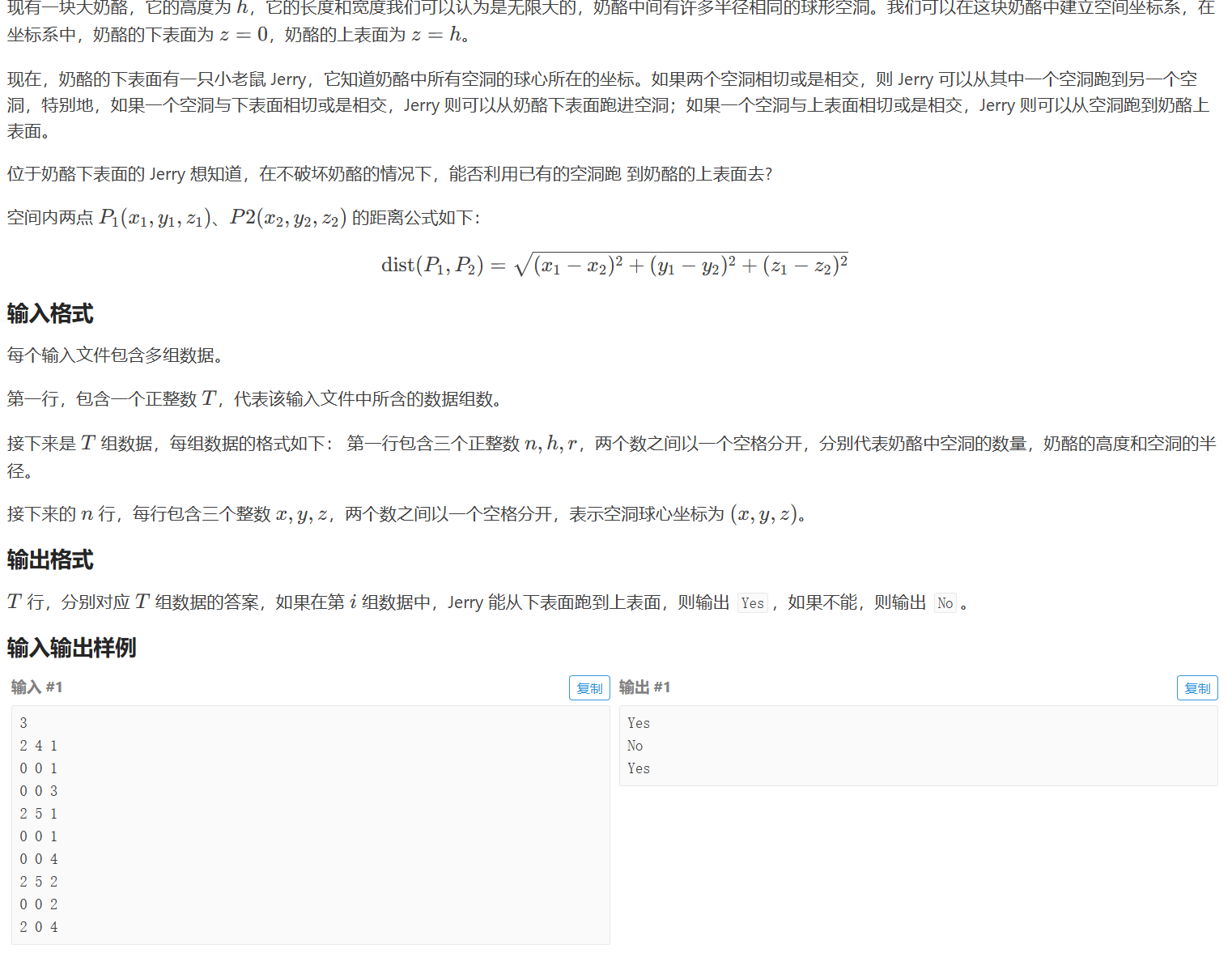
P3958 [NOIP 2017 提高组] 奶酪

这题的关键是识别出这是属于并查集的答案 ，同时注意对于大数据long long类型的比较

思路：

  1. 将每个洞虚拟化为并查集集合，并记录连接底部和顶部的洞。
  2. 双重循环，遍历合并能连通的洞
  3. 判断连接底部和顶部的点是否位于同一集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
#include <utility>
using namespace std;
typedef long long LL;
const int N = 100001; 

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;


int T;
int n,h,r;
long long point[N][3];
int toppoint[N], lowpoint[N]; //记录最高最低点
int p[N];


int lowcnt = 0;
int topcnt = 0;


int find(int x){
    if(p[x] != x)
        p[x] = find(p[x]);
    return p[x];
}



bool distin(int i, int j)
{
    return  4LL*r*r >=  ((point[i][0]-point[j][0])*(point[i][0]-point[j][0]) 
     + (point[i][1]-point[j][1])* (point[i][1]-point[j][1])
     +(point[i][2]-point[j][2])*(point[i][2]-point[j][2]) ) ? true : false;
}




void solve() {
    lowcnt = 0;
    topcnt = 0;
    cin >> n >> h >> r;
 
    

    for(int i = 1; i <= n; i++)
        p[i] = i;

    for(int i = 1; i <=n; i++)
    {
        cin >> point[i][0] >>point[i][1]  >> point[i][2] ;
        if(point[i][2] - r <= 0)  lowpoint[lowcnt++] = i;
        if(point[i][2]+r >= h)   toppoint[topcnt++] = i;
    }
    for(int i = 1; i <= n; i++)
    {
        for(int j = i+1; j <= n; j++)
        {
                if(distin(i,j))
                    p[find(j)] = find(i);
                    // int x = find(i);
                    // int y = find(j);
                    // if (x != y) p[x] = y;
        }
    }
    for(int i = 0; i < topcnt;i++)
    {
        for(int j = 0; j < lowcnt; j++)
        {
                if(find(toppoint[i]) == find(lowpoint[j]))
                {
                    cout << "Yes" << endl;
                    return ;
                }
        }
    }
    cout << "No" << endl;

}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> T;
    while(T--) {
       solve();
    }
}

堆

  • 插入一个数
  • 求当前集合最小值
  • 删除最小值

  • 删除或修改任意元素

  • 1为根，左儿子，2x，右儿子2x+1

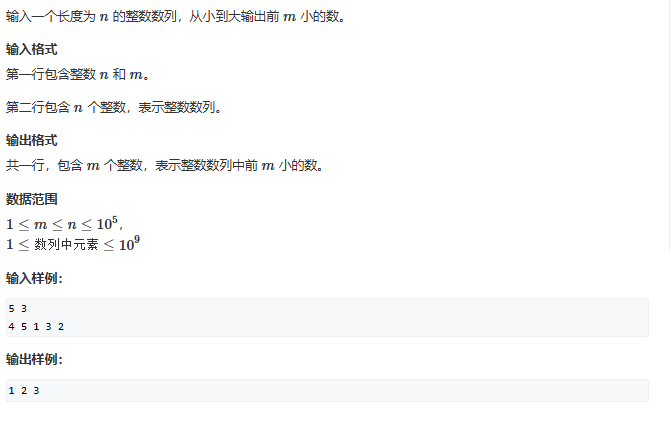
838. 堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

using namespace std;
int n, m, siz;
const int N = 100010;

int h[N];
void down(int u) {
  int t = u;
  if (h[2 * u] < h[t] && 2 * u <= siz)
    t = 2 * u;
  if (h[2 * u + 1] < h[t] && (2 * u + 1) <= siz)
    t = 2 * u + 1;
  if (t != u) {
    swap(h[t], h[u]);
    //别忘了递归
    down(t);
  }
}
int main() {
  cin >> n >> m;
  for (int i = 1; i <= n; i++)
    cin >> h[i]; //从1开始

  siz = n; // 将 siz 初始化为 n      要在down前初始化

  for (int i = n / 2; i >= 1; i--)
    down(i);

  for (int i = 0; i < m; i++) {
    cout << h[1] << " ";
    h[1] = h[siz--];

    down(1);
  }
}

839. 模拟堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include<iostream>
#include<algorithm>
using namespace std;

const int N=1e5+10;
int h[N];   //堆
int ph[N];  //存放第k个插入点的下标
int hp[N];  //存放堆中点的插入次序
int cur_size;   //size 记录的是堆当前的数据多少,即堆的最后一个元素





void heap_swap(int a,int b)
{
    swap(h[a],h[b]);            //交换堆中两个元素的值
    swap(hp[a],hp[b]);          //交换插入次序
    swap(ph[hp[a]],ph[hp[b]])  ;   //交换插入点的下标
}



void down(int u)
{
    int t=u;
    if(u*2<=cur_size&&h[t]>h[u*2]) t=u*2;
    if(u*2+1<=cur_size&&h[t]>h[u*2+1])  t=u*2+1;
    if(u!=t)
    {
        heap_swap(u,t);
        down(t);
    }
}
void up(int u)
{
    if(u/2>0&&h[u]<h[u/2]) 
    {
        heap_swap(u,u/2);
        up(u>>1);
    }
}




int main()
{
    int n;
    cin >> n;
    int m = 0;        //m用来记录插入的数的个数
      while(n--)
    {
        string op;
        int k,x;
        cin>>op;
        if(op=="I")
        {
            cin>>x;
            m++;
            h[++cur_size]=x;    //置于堆的最后
            ph[m]=cur_size;     //记录第k个插入点的下标
            hp[cur_size]=m;     //记录插入次序
            //down(size);
            up(cur_size);
        }
        else if(op=="PM")    cout<<h[1]<<endl;
        else if(op=="DM")
        {
            heap_swap(1,cur_size);
            cur_size--;
            down(1);
        }
        else if(op=="D")
        {
            cin>>k;
            int u=ph[k];                //这里一定要用u=ph[k]保存第k个插入点的下标
            heap_swap(u,cur_size);          //因为在此处heap_swap操作后ph[k]的值已经发生 
            cur_size--;                    //如果在up,down操作中仍然使用ph[k]作为参数就会发生错误
            up(u);
           down(u);
        }
        else if(op=="C")
        {
            cin>>k>>x;
            h[ph[k]]=x;                 //此处由于未涉及heap_swap操作且下面的up、down操作只会发生一个所以
            down(ph[k]);                //所以可直接传入ph[k]作为参数
            up(ph[k]);
        }

    }
    return 0;


}

//TODO

哈希表

840. 模拟散列表

拉链法：

数组 +（重复元素插入链表）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100003;

int h[N], e[N], ne[N], idx;

void insert(int x) //链式前向星
{
  int k = (x % N + N) % N;
  //(x + N)%N;  不能采用以下方式因为x可能远大于N的范围
  e[idx] = x;     //插入元素
  ne[idx] = h[k]; //将插入的元素插入到链表的头部
  h[k] = idx++;   //指向最后一个插入的元素
}

bool find(int x) {
  int pos = (x % N + N) % N;
  for (int i = h[pos]; i != -1; i = ne[i]) {
    if (x == e[i])
      return true;
  }
  return false;
}

int main() {
  memset(h, -1, sizeof(h));
  int n;
  scanf("%d", &n);
  while (n--) {
    char op[2];
    int x;
    scanf("%s%d", op, &x);
    if (op[0] == 'I')
      insert(x);
    else if (op[0] == 'Q') {
      if (find(x))
        printf("Yes\n");
      else
        printf("No\n");
    }
  }
}
开放寻址法

N应该取题目要求的两到三倍

1
2
3
4
 (x % N + N) % N;		
第一个x % N可能得到负数(如果x为负)
+ N确保结果为正
第二个% N确保结果在正确范围内
cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstring>
#include <iostream>

using namespace std;

const int N = 200003, null = 0x3f3f3f3f;    
//0x3f3f3f3f * 2 = 2122219134，无穷大相加依然不会溢出。

int h[N];

int find(int x) {
  int pos = (x % N + N) % N;		
  while(h[pos] != null && h[pos] != x)
  {
    pos++;
    if(pos == N)
      pos = 0;
  }
  return pos;
}

int main() {
  memset(h, 0x3f, sizeof(h));
  int n;
  scanf("%d", &n);
  while (n--) {
    char op[2];
    int x;
    scanf("%s%d", op, &x);
    if (op[0] == 'I')
        h[find(x)] = x;
    else if (op[0] == 'Q') {
      if (h[find(x)] != null)
        printf("Yes\n");
      else
        printf("No\n");
    }
  }
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
n = int(input())

null = 0x3f3f3f3f
arr =  [null]*n*3


# 返回第一个满足以下条件的位置：
# 槽位为空(h[pos] == null)，可以插入新元素
# 槽位已包含x(h[pos] == x)，表示元素已存在
def find(x):
    pos = (x%n+n)%n
    while arr[pos] !=null and  arr[pos] != x:
        pos = pos+1
        if pos == n:
            pos = 0
    return pos

for i in range(n):
    op, x = input().split()
    x = int(x)
    if op == 'I':
        arr[find(x)] = x
    else:
        pos = find(x)
        if arr[pos] != null:
            print('Yes')
        else:
            print('No')

AcWing 841. 字符串哈希（字符串前缀哈希法）

AcWing 841. 字符串哈希 【公式助理解】 - AcWing

cpp

P = 13331,Q=2^64

  • 创建方程
    • h[i] = [h[i-1]*P+ ord(arr[i-1])] %mod, 创建哈希 （注意下标，防止查询时数组越界）
    • p[i] = p[i]P % mod p``i次方
  • 查询方程h[r] - h[l-1] * p[r-l+1] l-1>=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include <string>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+5,P = 13331;
ULL h[N],p[N];

ULL query(int l,int r){
    return h[r] - h[l - 1]*p[r - l + 1];
}
int main()
{
    int n, m;
    cin >> n >> m;
    string s;
    cin >> s;
    p[0] = 1;
    h[0] = 0;
    for(int i =0 ; i < s.size(); i++)
    {
        h[i + 1] = h[i] * P + s[i];
        p[i + 1] = p[i] * P;
    }
    while(m--)
    {
        int l1, l2, r1, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if(query(l1, r1) == query(l2, r2))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    
}

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
n,m = map(int,input().split())

mod = 10**9+7
P = 13331

h = [0]*(n+10)
p = [1]*(n+10)

def query(l,r):
    return (h[r] - h[l-1]*p[r-l+1])%mod     #求区间哈希值,pyhon无法利用ull性质，需要手动取模。


s = input()

for i in range(1,n+1):  #从第一位开始预处理
    p[i] = (p[i-1]*P) % mod  #预处理p的i次方
    h[i] = (h[i-1]*P + ord(s[i-1])) % mod #字符串哈希
    
    
for _ in range(m):
    l1,r1,l2,r2 = map(int,input().split())
    if query(l1,r1) == query(l2,r2):
        print('Yes')
    else:
        print('No')