[toc]

基础课

图的存储

cpp

链式前向星

1
2
3
4
5
6
7
8
9
10
11
12
int h[N], e[M], ne[M],  idx;
//idx表示第n条边
//h[N] : 表示 第 i 个节点的 第一条边的 idx
//ne[M] : 表示 与 第 idx 条边 的 下一条边 的 idx
//e[M] : 表示 第idx 条边的 终点

void add(int a,int b)
{
    e[idx] =  b;            //记录终点节点
    ne[idx] = h[a];        //相当于插入链表 ，将此节点后面的值传进来
    h[a] = idx ++;         //h[a]指向当前新增的节点
}

python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
graph = {}
n = int(input().strip())
for i in range(n-1):
    a, b = map(int, input().split())
    if a not in graph:
        graph[a] = [b]
    else:
        graph[a].append(b)
    ### 存储无向图,建双向边
    if b not in graph:
        graph[b] = [a]
    else:
        graph[b].append(a)
# 初始化状态数组
st = [False for i in range(n+1)]

def dfs(u):
    st[u] = True

    for i in range(graph[u]):
        if not st[i]:
            dfs(i)

数据结构 空间
DFS stack O(n)
BFS queue 最短路
算法 优点 缺点 适用问题
DFS 空间效率高，适合深层遍历 不保证最短路径，可能栈溢出 路径搜索、回溯、拓扑排序
BFS 保证最短路径，适合层次遍历 空间占用大（存储整层节点） 最短路径、扩散问题、层次分析

DFS

  • 采用stack
  • 回溯——恢复状态
  • 剪枝——提前回溯

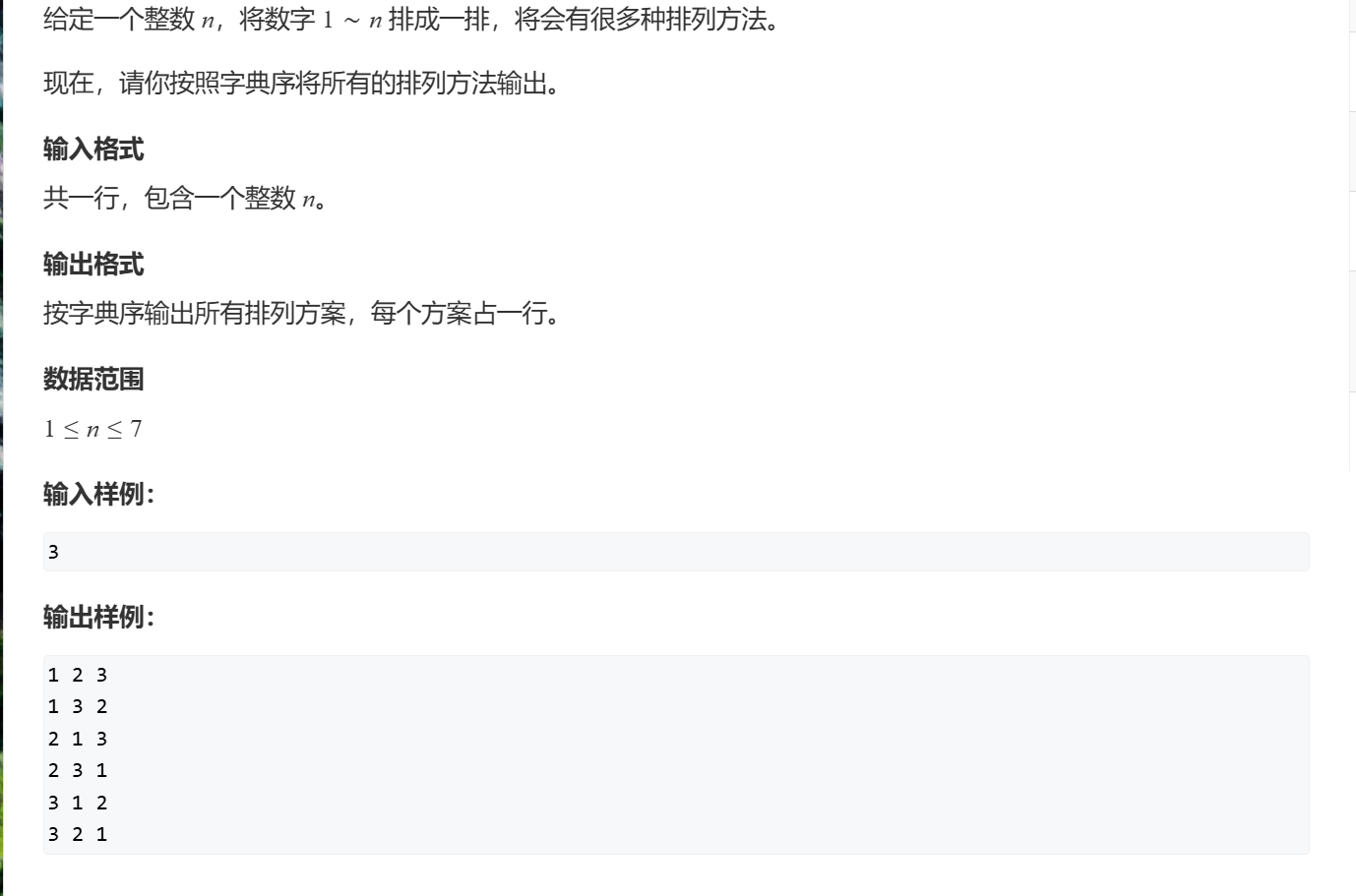
遇到诸如放置、字典序等可使用深搜输出全部组合。

AcWing 842. 排列数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>

using namespace std;

const int N = 100;

int n;  //记录深度

int path[N];
int st[N];

void dfs(int u)	//u控制路径长度和路径索引
{
    if (u== n)  //path形成，输出
        {
            for (int i = 0 ;i < n; i ++)
            printf("%d", path[i]);
            puts("");
            return;
        }
    for (int i = 1; i <= n; i ++)	//可以访问的子路径
        {
            if(!st[i])
                path[u] = i;	//记录路径
                st[i] = true;
                dfs(u + 1);
                st[i] = false;
        }
}


int main()
{   
  
    cin >> n;
  
    dfs(0);
    
    return 0;
}

AcWing 843. n-皇后问题

通过枚举每行（若n皇后问题能解决，则每行必有一个皇后），再通过行列表示主对角线和副对角线，判断条件符合则递归调用dfs。

  • 所有主对角线上的点，其坐标差 i−j 相同。(x+1)-(y+1) = x-y
  • 所有副对角线上的点，其坐标和 i+j 相同。(x-1)-(y-1) = x+y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>

using namespace std;
const int N  = 200; 
int n;
char g[N][N];

bool col[N], dg[N], udg[N];
//列    column
//行    line
//对角线    diagonal


void dfs(int u)
{
    if (u == n)  
        {
            for (int i = 0 ;i < n; i ++)    puts(g[i]); //char* 型指针
            puts("");
            return;
        }
    for (int i = 0; i < n; i ++)       //枚举列
        {
            if(!col[i] && !dg[u + i] && !udg[n - u + i])
               { 
                g[u][i] = 'Q';
                col[i] = dg[u + i] = udg[n - u + i] = true;
                dfs(u + 1);
                col[i] = dg[u + i] = udg[n - u + i] = false;
                g[u][i] =  '.';
               }
        }
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n; j ++)
            g[i][j] = '.';
    dfs(0);
    return 0;
}

BFS

  • 采用queue
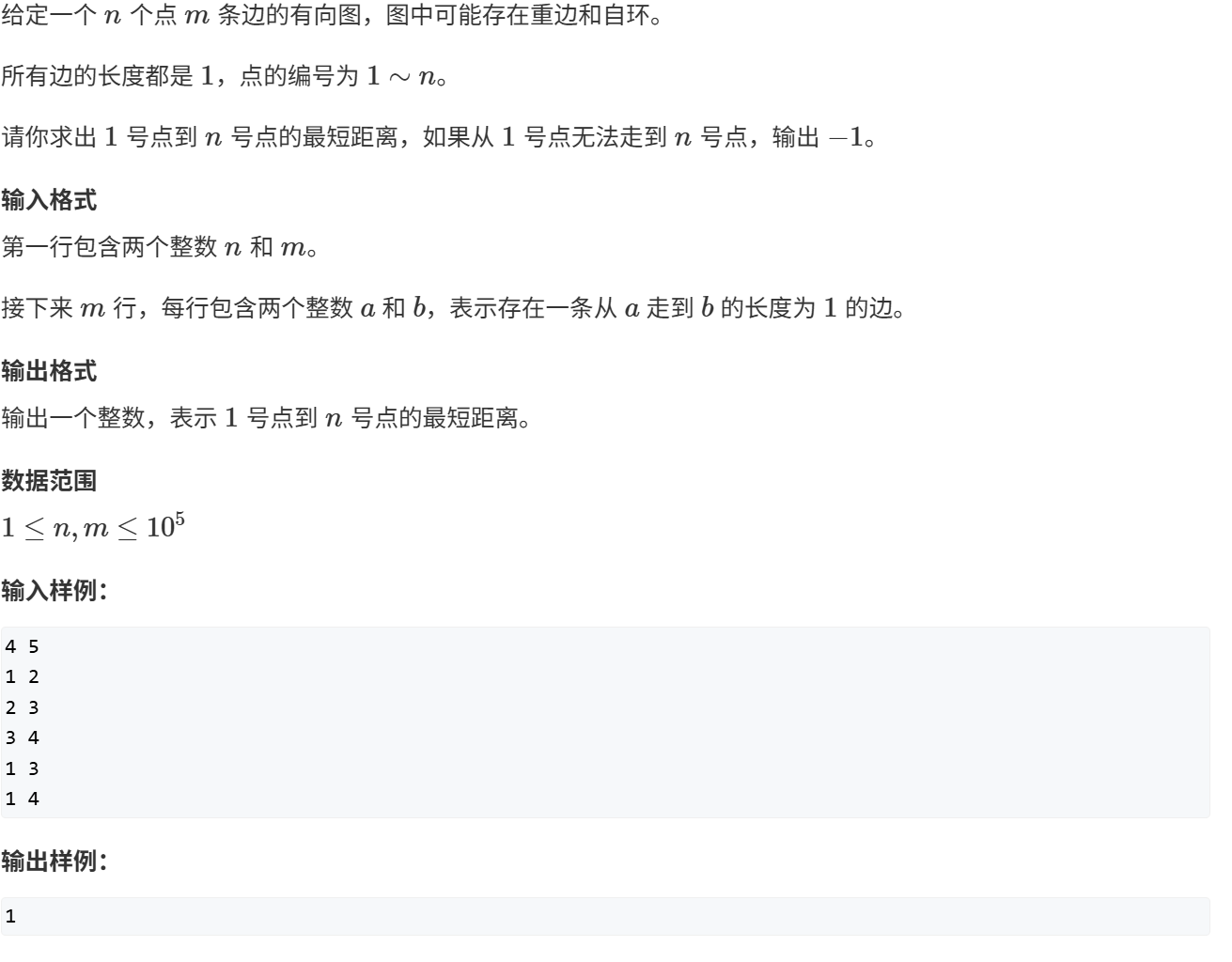
  • 边权都为1时，为最短路径
  • DP是特殊的最短路问题

AcWing 844. 走迷宫

BFS算法相当于在有m个后继点的点处分裂为m个小鼠，同时将访问过的点在数组上标定距离（该距离是最小值，因为其他点在相同步数下并不能访问该点），最后返回要求的坐标即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <utility>
#include <queue>

using namespace std;
typedef long long LL;
const int N = 1e2 +10; 
int arr[N][N];
int d[N][N];    
int n,m;
typedef pair<int,int> PA;
typedef pair<int,PA> PA2  ;

int xway[] = {-1,0,0,1};
int yway[] = {0,-1,1,0};


void  bfs(int x, int y)
{
    
    queue<PA> qu;
    qu.push({x,y});
    //qu.push({0,{x,y}});       使用d[][]来存储距离提升程序运行速率。
    while(!qu.empty())
    {
        auto tmp = qu.front();
        qu.pop();
        for(int i = 0; i < 4; i++)
        {
            int xx = tmp.first + xway[i];
            int yy = tmp.second + yway[i];
            if(xx > 0 && xx <= n && yy > 0 && yy <= m && arr[xx][yy]!= 1 && d[xx][yy]==0)
            {
                d[xx][yy] = d[tmp.first][tmp.second] + 1;
                qu.push({xx,yy});
            }
        }
    }

}


int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> arr[i][j];
    bfs(1,1);
    cout << d[n][m] << endl;
  
}

AcWing 845. 八数码

字符串上BFS这题我们从输入的状态出发，直到到达最终的状态，本质是bfs算法，通过枚举所有可能的变换，在变换的基础上再进行枚举，直到匹配最终状态。

1
2
3
4
5
6
7
8
9
记录一个错误的方向数组
int way[] = {-3,+3,-1,1};

1 2 3
x 4 6
7 5 8

若取x+way[2]，则swap(x,3)不符合题意
因此对于该题，应该先转化为x，y的
  • 通过<unordered_map>存储该状态的最短路径
    • 若.count()存在，说明已经访问过且当前路径不是最短路径
    • 若!.count()，则说明未访问该路径，添加到map
    • 为什么使用<unordered_map>
      • 能保证O(1)的访问时间，但是不能进行排序
      • <map>访问时间为(logn)，按键自动排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <queue>
#include <string>
#include <unordered_map>
using namespace std;

string finnal = "12345678x";
unordered_map<string, int> un_map; //存放状态
queue<string> status;              //存放小鼠

int bfs(string st) {
  un_map[st] = 0;
  status.push(st);

  int xway[4] = {-1, 0, 1, 0};
  int yway[4] = {0, -1, 0, 1};

  while (status.size()) {
    string tmp = status.front();
    status.pop();
    int pos = tmp.find('x');
    int x = pos / 3;
    int y = pos % 3;
    int distance = un_map[tmp];
    if (tmp == finnal)
      return distance;

    for (int i = 0; i < 4; i++) {
      int a = x + xway[i], b = y + yway[i];		//行列移动转化为字符串加减
      if (a >= 0 && a < 3 && b >= 0 && b < 3) {
        swap(tmp[pos], tmp[3 * a + b]);
        if (!un_map.count(tmp)) {
          un_map[tmp] = distance + 1;
          status.push(tmp);
        }
        swap(tmp[pos], tmp[3 * a + b]); //恢复现场
      }
    }
  }
  return -1;
}

int main() {
  string st;
  for (int i = 0; i < 9; i++) {
    char tmp;
    cin >> tmp;
    st += tmp;
  }
  cout << bfs(st) << endl;
  return 0;
}

树与图的深度优先遍历

acwing846 树的重心

cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010, M = N * 2;

int n;

int ans = N;

int h[N], e[M], ne[M],  idx;
//idx表示第n条边
//h[N] : 表示 第 i 个节点的 第一条边的 idx
//ne[M] : 表示 与 第 idx 条边 的 下一条边 的 idx
//e[M] : 表示 第idx 条边的 终点

bool st[N];	·//节点是否被访问过，访问过则标记为true

void add(int a,int b)
{
    e[idx] =  b;            //记录终点节点
    ne[idx] = h[a];        //相当于插入链表 ，将此节点后面的值传进来
    h[a] = idx ++;         //h[a]指向当前新增的节点
}

int dfs(int u) {
    st[u] = true;    // 标记当前节点已访问

    int sum = 1;     // 当前子树大小（包含自己）
    int res = 0;     // 记录删除 u 后，各连通块的最大节点数

    // 遍历 u 的所有邻接节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {  
            int s = dfs(j);    // 递归计算以 j 为根的子树大小
            res = max(res, s); // 更新最大子树大小
            sum += s;          // 累加子树大小
        }
    }

    // 计算父节点方向的连通块大小（总节点数 - 当前子树大小）
    res = max(res, n - sum);

    // 更新全局答案（所有节点的 res 的最小值）
    ans = min(ans, res);

    return sum;  
}

int main()
{
    memset (h, -1, sizeof h);
    int a,b;
    cin >> n;
    for (int i = 0;i < n ; i ++)
        {
            cin >> a >>b;
            add(a, b), add(b, a);
        }

    dfs(1);
    cout << ans << endl;
    return 0;
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
n = int(input().strip())
st = [False for _ in range(n+1)]
graph = {}
res = n
def dfs(u):
    global res
    st[u] = True	
    size = 0
    sumNode = 0
    for v in graph[u]:
        if not st[v]:
            s = dfs(v)
            sumNode = sumNode+ s
            size = max(size, s)	#
    size = max(size, n-sumNode-1)
    res = min(res, size)
    return sumNode+1

for _ in range(n-1):
    a, b = map(int, input().split())
    if a not in graph:      #a到b
        graph[a] = [b]
    else:
        graph[a].append(b)  
    if b not in graph:       #b到a
        graph[b] = [a]
    else:
        graph[b].append(a)  

dfs(3)
print(res)

树与图的广度优先遍历

AcWing 847. 图中点的层次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
using namespace std;
typedef pair<int,int> PII;
const int N = 100010;
int h[N],ne[N],e[N],idx,st[N];
int dist[N];
int n,m;

int add(int a,int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void bfs()
{
    memset(dist,0x3f3f3f3f,sizeof dist);
    dist[1] = 0;
    st[1] = 1;
    queue<int> q;
    q.push(1);
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = h[t];i!=-1;i = ne[i])
        {
            int  j = e[i];
            if(!st[j])
            {
                st[j] = 1;
                dist[j] = dist[t]+1;
                q.push(j);
            }
        }
    }
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    for(int i = 0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    bfs();
    if(dist[n]==0x3f3f3f3f)
    cout<<-1;
    else
    cout<<dist[n];
    return 0;
}

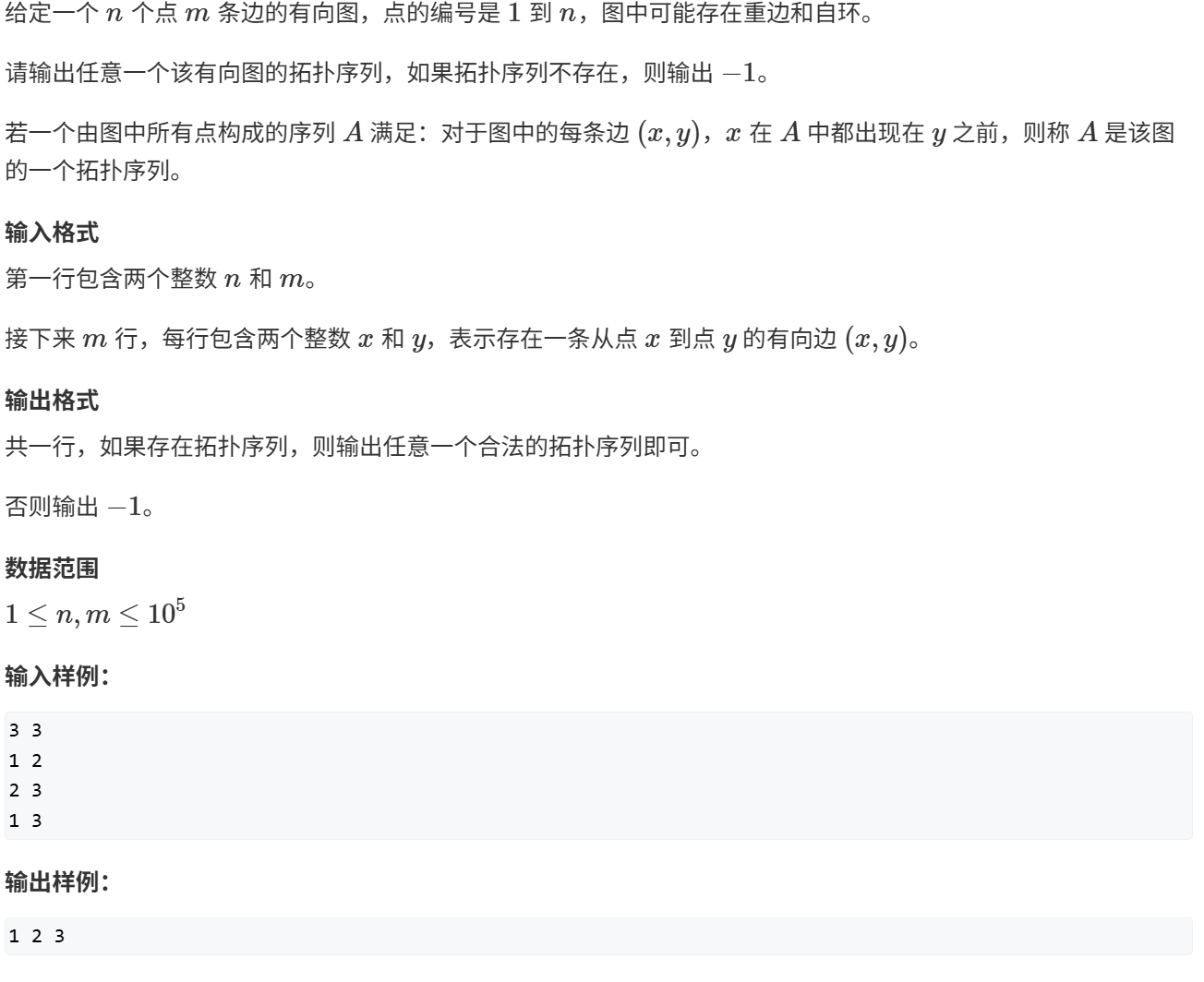
拓扑序列(有向图)

  • 核心要求：如果存在从 u 到 v 的路径，则 u 必须在 v 之前。即“事件执行的合理顺序”

  • 有环不存在拓扑序列

  • 一个有向无环图（拓扑图），一定至少有一个入度为0的点 —>一定存在拓扑序列
  • 使用数组模拟队列输出路径
  1. 统计所有节点的入度（指向该节点的边数）。
  2. 将入度为 0 的节点加入队列。
  3. 依次取出队列中的节点，并“删除”它（将其邻接节点的入度减 1）。
  4. 若邻接节点入度变为 0，则加入队列。
  5. 重复直到队列为空。若所有节点被处理，则得到拓扑序列；否则图中存在环。

AcWing 848. 有向图的拓扑序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <cstring>
#include <iostream>
#include <utility>
using namespace std;
typedef long long LL;
const int N = 1e5 +10; 
int arr[N];

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;

int h[N], e[N], ne[N], idx ;
int q[N], d[N];
int hh = 0,tt = -1;

void add(int a, int b)
{
    e[idx] = b;     
    ne[idx] = h[a];     
    h[a] = idx ++;
}

void topsort()
{
   for(int i = 1; i<=n;i++)
   {
        if(!d[i])
            q[++tt] = i;    //将入度为0的点入队
   }
   while(hh<=tt)
   {
        int p = q[hh++];
        for(int i = h[p];i!=-1; i = ne[i])
        {
            int j = e[i];
            d[j] --;
            if(d[j] == 0)   //入度减为0
            {
                q[++tt] = j;
            }
        }
   }
   return ;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 0; i< m; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a,b);
        d[b]++; //入度++
    }
    topsort();
    if(tt == n-1)   //所有点入度都减到0
        for(int i = 0; i< n;i++)
        {
            cout << q[i] <<" ";
        }
    else
        cout << -1 << endl;

   // cout << hh << tt << endl;
    return 0;
}

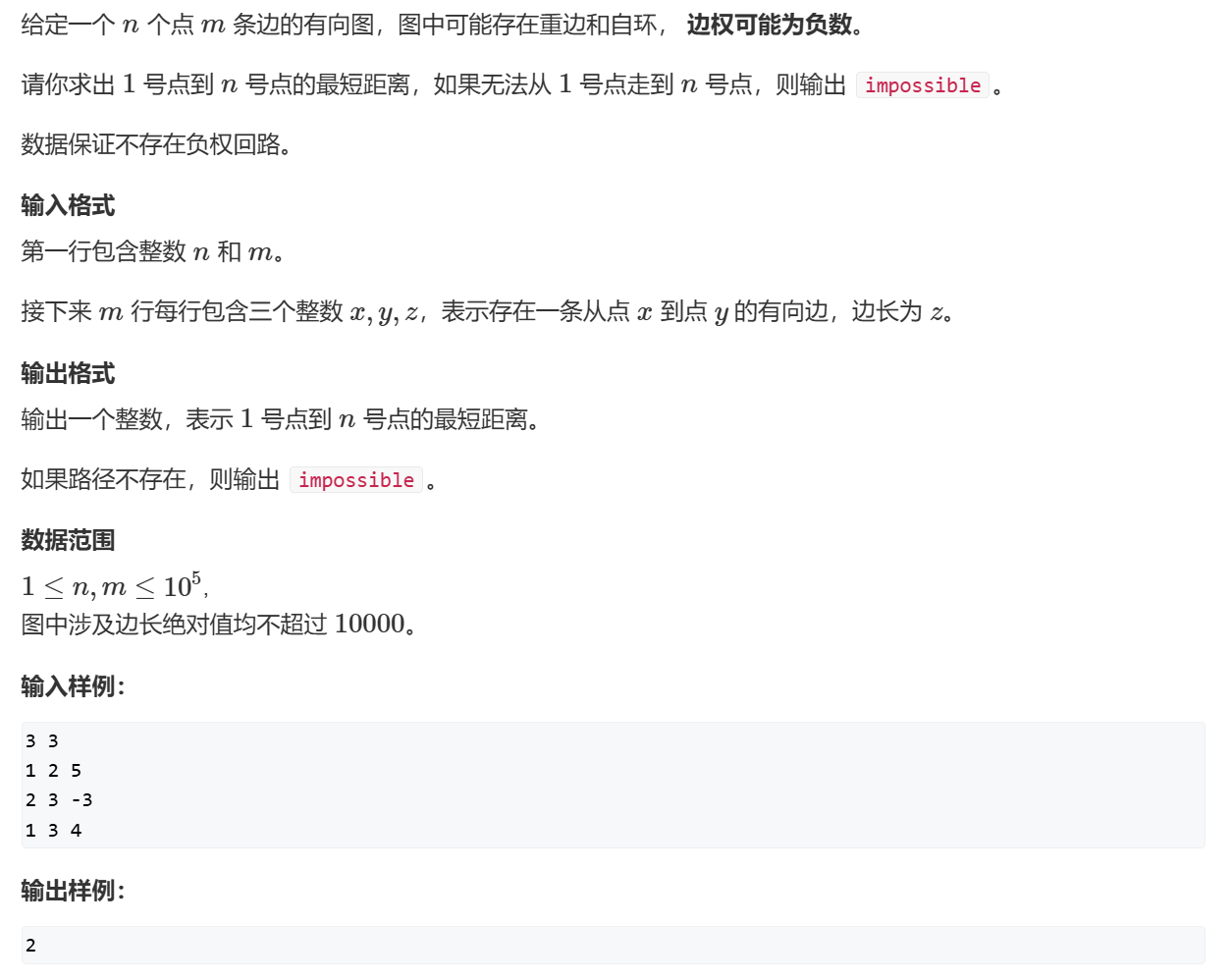
最短路问题

单源最短路

Dijkstra是用最短的边去更新其他边，而spfa是上次更新的终点去更新其他边，Bellman-Ford则暴力每次更新所有边

所有边权都为正数
算法 时间复杂度 适用场景 核心思想
朴素Dijkstra O(n²) 稠密图 每次选择当前距离起点最近的未确定节点，贪心扩展。
堆优化Dijkstra O(mlogn) 稀疏图 用优先队列维护未确定节点的最小距离，避免线性扫描。
存在负权边
算法 时间复杂度 适用场景 核心思想
Bellman-Ford O(nm) 任意图 对所有边进行松弛操作，重复 n-1 次保证收敛。
SPFA 平均 O(m)，最坏 O(nm) 负权图但无负环（负环权值之和为负数） 队列优化 Bellman-Ford，仅松弛距离被更新的节点。

多源汇点最短路

Floyd算法 O()

  • 动态规划：逐步允许通过中间节点 k 更新任意两点间的最短距离。
  • 不能处理负环

Dijkstra

AcWing 849. Dijkstra求最短路 I

朴素Dijkstra算法

  1. 将除起点外的距离都置为无穷
  2. 选取当前点到另一未访问且距离最短的边
  3. 更新所有点到起点的距离
  4. 重复2——3，直到到达终点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 510;

int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N];  //用于记录该点的最短距离是否已经确定

int n, m;

int Dijkstra() {
  memset(dist, 0x3f, sizeof dist);
  dist[1] = 0;
  for (int i = 0; i < n; i++) //对每个点确定一次最短距离
  {
    int t = -1;
    for (int j = 1; j <= n; j++) {
      if (!st[j] && (t == -1 || dist[t] > dist[j]))     //选择没有访问且距离最短的下一点
        t = j;
    }
    st[t] = true;       //设置为已访问

    for (int j = 1; j <= n; j++) {
      dist[j] = min(dist[j], dist[t] + g[t][j]);   //更新与t有关点的最短距离
    }
  }

  if (dist[n] == 0x3f3f3f3f)
    return -1; //如果第n个点路径为无穷大即不存在最低路径
  return dist[n];
}

int main() {
  cin >> n >> m;
  memset(g, 0x3f, sizeof g);

  while (m--) {
    int a, b, c;
    cin >> a >> b >> c;
    //自环不会影响Dijkstra
    g[a][b] = min(g[a][b], c);  //重边的话选择最短边
  }
  cout << Dijkstra() << endl;
  return 0;
}

AcWing 850. Dijkstra求最短路 II

使用优先队列模拟堆来实现距离的排序，同时再出队时遍历从该点出发的边实现更新最短距离值。

cpp
  • 使用小根堆（priority_queue）快速获取当前未处理节点中距离最小的节点。
  • 相较于朴素版dijkstra算法，堆优化版通过邻接表遍历自动覆盖来处理重边，自环若权值为正则不影响结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 150010;

// 稀疏图用邻接表来存
int h[N], e[N], ne[N], idx;
int w[N]; // 用来存权重
int dist[N];
bool st[N];

int n, m;

void add(int a, int b, int c) {p
  e[idx] = b;     //存终点
  ne[idx] = h[a]; //存上一条边索引
  w[idx] = c;     //存权重
  h[a] = idx++;   //存下标
}

int dijkstra() {
  memset(dist, 0x3f, sizeof dist);
  dist[1] = 0;
  priority_queue<PII, vector<PII>, greater<PII>> heap;	//小根堆
  heap.push({0, 1}); // 存入{距离, 节点}，按距离排序
  while (heap.size()) {
    auto t = heap.top();
    heap.pop();
    int distance = t.first, node = t.second;

    if (st[node])
      continue; // 如果节点被访问过，则跳过
    st[node] = true;

    for (int i = h[node]; i != -1; i = ne[i]) { //遍历从该节点出发，所有边
      int j = e[i];
      if (dist[j] > dist[node] + w[i]) {	// 松弛操作
        dist[j] = dist[node] + w[i];
        heap.push({dist[j], j});
      }
    }
  }
  if (dist[n] == 0x3f3f3f3f)
    return -1;
  else
    return dist[n];
}

int main() {
  memset(h, -1, sizeof(h));
  scanf("%d%d", &n, &m);

  while (m--) {
    int x, y, c;
    scanf("%d%d%d", &x, &y, &c);
    add(x, y, c);
  }

  cout << dijkstra() << endl;

  return 0;
}
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import os
import heapq
import sys
import math
sys.setrecursionlimit(10000)

input = lambda: sys.stdin.readline().strip()
n,m = map(int,input().split())

# 防止该点不存在导致程序crash
graph = {i: [] for i in range(1,n+10)}

inf = float(math.inf)

dist = [inf] * (n+10)
st = [False] * (n+10)

def dij():
    hp = []
    heapq.heappush(hp,[0,1])
    while hp:
        dis, point = heapq.heappop(hp)
        if st[point]:
            continue
        st[point] = True
        
        for v,w in graph[point]:
            if dist[v] > dis + w:
                dist[v] = dis + w
                heapq.heappush(hp,(dist[v],v))
    

for i in range(m):
    x,y,z = map(int,input().split())
    graph[x].append((y,z))
    
dij()    
if dist[n] == inf:
    print(-1)
else:
    print(dist[n])

bellman-ford （有边数限制）

AcWing 853. 有边数限制的最短路

连续进行松弛，在每次松弛时把每条边都更新一下。

若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge {
    int a;
    int b;
    int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包含k条边


void bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < k; i++)
    {
        memcpy(back, dist, sizeof dist);
        //对于每个点，都需要对每条边进行松弛操作
        //我们需要把i-1次的迭代结果保存下来，保每次迭代只基于上一轮的结果（）
        //A→B→C，若直接更新 dist，可能在同一轮中同时更新 B 和 C，违反“最多经过 k 条边”的限制。
        for (int i = 0; i < m; i++) {
            int a = e[i].a, b = e[i].b, w = e[i].w;
            dist[b] = min(dist[b], back[a] + w);        //使用备份更新最短距离
        }
    }
}


int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    bellman_ford();
   
    if(dist[n]>0x3f3f3f3f/2) //若无法到达n号点，但x,n存在且为负值，则在每次枚举点时都会更新n的距离，使得距离小于0x3f3f3f3f
        puts("impossible");
    else printf("%d",dist[n]);

    return 0;
}

spfa

AcWing 851. spfa求最短路

  • 只有当一个点的前驱结点更新了，该节点才会得到更新 —>创建一个队列每一次加入距离被更新的结点。
  • st数组的作用：判断当前的点是否已经加入到队列中，减少不必要的遍历
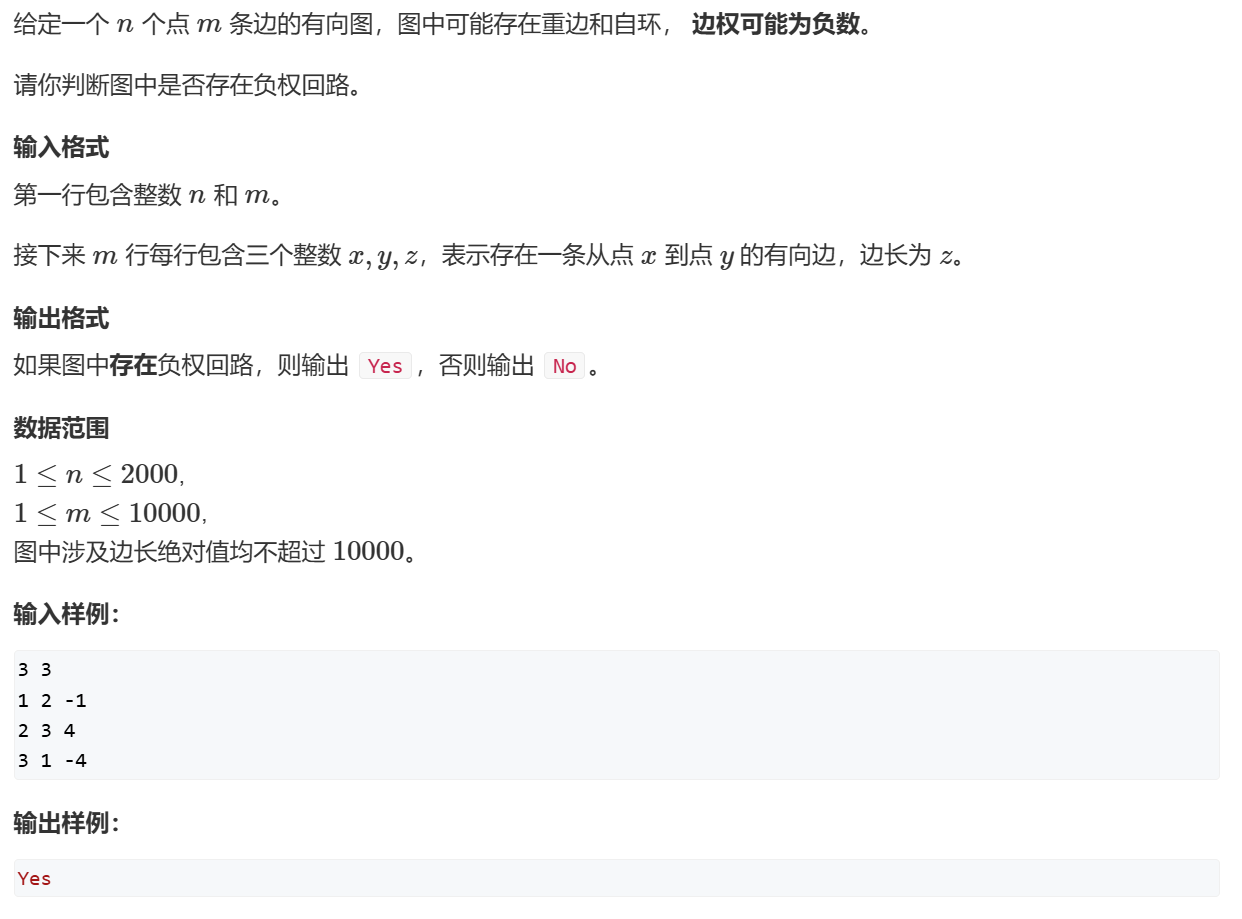
  • 有负权回路SPFA会死循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];     

void add(int a, int b, int c){
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx++;
}


int spfa(){
    memset(dist, 0x3f, sizeof dist);
    queue<int> q;
    q.push(1);
    dist[1] = 0;
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;     
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])  ///当前已经加入队列的结点，无需再次加入队列
                    {
                        st[j] = true;
                        q.push(j);
                    }
            }
        }
    }
    return dist[n];
}



int main(){
    memset(h, -1, sizeof h);
    memset(dist, 0x3f, sizeof dist);
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < m; i++){
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
    }
    spfa();
    if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷，则不能到达,因为spfa只遍历相连的边，而Bellman_ford遍历所有边 
        cout << "impossible";
    else cout << dist[n];
    return 0;
}

AcWing 852. spfa判断负环

统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环

spfa
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

const int N = 2e3 + 10, M = 1e4 + 10;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
bool st[N];      // 是否在队列中
int dist[N];     // 到起点的最短距离
int cnt[N];      // 最短路径的边数

void add(int a, int b, int c) {
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool spfa() {
    queue<int> q;
    // 初始化：所有节点入队，防止非连通图漏判
    for (int i = 1; i <= n; i++) {
        q.push(i);
        st[i] = true;
    }

    while (!q.empty()) {
        int t = q.front();
        q.pop();
        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;

                // 根据 Bellman-Ford，最短路径最多 n-1 条边
                // 如果 cnt[j] >= n，说明存在负环
                if (cnt[j] >= n)
                    return true;

                // 如果 j 不在队列中，则入队
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    if (spfa())
        cout << "Yes";
    else
        cout << "No";

    return 0;
}
bellman-ford
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;

const int N = 2005,M = 1e4 + 5,INF = 0x3f3f3f3f;
struct edge
{
    int a,b,c;
}e[M];
int n,m,dis[N];

string bellman()
{
    memset(dis,0x3f,sizeof dis);
    dis[1] = 0;

    bool flag = true;
    int cnt = 0;
    while(flag)
    {
        flag = false;
        cnt++;
        if(cnt > n) return "Yes";  //迭代超过n次根据抽屉原理出现了n+1个点既出现了负环
        for(int i=0;i<m;i++)
        {
            int a = e[i].a,b = e[i].b,c = e[i].c;
            if(dis[b] > dis[a] + c)		
            {
                flag = true;
                dis[b] = dis[a] + c;
            }
        }
    }
    return "No";
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        e[i] = {a,b,c};
    }
    cout<<bellman()<<endl;
    return 0;
}

floyd

Floyd-Warshall 算法的动态规划状态转移方程可以表示为：

  • ：允许使用前 k 个节点作为中转时，节点 i 到 j 的最短距离。

状态转移：

  • 不经过 k：保持

  • 经过 k：路径分解为 $i \rightarrow k$ 和 $k \rightarrow j$ 的最短距离之和

滚动数组优化：

d[i][j] ← min(d[i][j], d[i][k] + d[k][j])

  • 通过就地更新，将三维 状态压缩为二维。

AcWing 854. Floyd求最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <utility>
using namespace std;
typedef long long LL;
const int N = 2e4 +10; 
int d[N][N];
int INF = 1e9;

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m,Q;

void floyd()
{
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n >> m >> Q;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i == j) d[i][j] = 0;
            else d[i][j] = INF;
    while(m--)
    {
        int a,b,c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c);	 // 处理重边
    }
    floyd();
    while(Q--)
    {
        int a,b;
        cin >> a >> b;
        if(d[a][b] > INF/2) cout << "impossible" << endl;
        else cout << d[a][b] << endl;
    }
}

最小生成树

  • 普利姆算法（Prim）
    • 朴素版Prim O(n^2) 稠密图
    • 堆优化版Prim O(mlogn)
  • 克鲁斯卡尔算法（Kruskal） O(mlogm) 稀疏图

Prim

AcWing858. Prim算法求最小生成树

Prim算法：我们从其中一个点出发，遍历该点所有边，找到最小权值的边，然后加入集合，更新该边另一顶点引出的边（使从该边引出的节点可达）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N];
bool st[N]; // 记录每个节点是否已经被包含在最小生成树中


int prim()
{
    memset(dist, 0x3f, sizeof dist);
    int res = 0;
    for(int i = 0; i < n; i ++ )
    {
        int t = -1;
        for(int j = 1; j <= n; j ++ )
            if(!st[j] && (t == -1 || dist[t] > dist[j]))    //贪心，找到距离当前集合的最小边
                t = j;
        if(i && dist[t] == INF) return INF;  //点不可达，不能生成最小树

        // 更新必须放在for循环前,避免自环，且当t放入集合后，其dist[t]已经没有意义
        if(i)   res += dist[t]; // 如果不是第一个点，将其权值加入结果中    
        st[t] = true;    

        for(int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]);        // 更新 dist 数组，记录每个节点到当前生成树的最小距离
        //即将一些点变为可达的点
    }
    return res;
}


int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);    //取最短边，Prim算法针对无向图，因此赋值两次
    }

    int t = prim();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

AcWing 858. Prim算法求最小生成树：图解+详细代码注释（带上了保存路径） - AcWing

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510;
int g[N][N];//存储图
int dt[N];//存储各个节点到生成树的距离
int st[N];//节点是否被加入到生成树中
int pre[N];//节点的前去节点
int n, m;//n 个节点，m 条边

void prim()
{
    memset(dt,0x3f, sizeof(dt));//初始化距离数组为一个很大的数（10亿左右）
    int res= 0;
    dt[1] = 0;//从 1 号节点开始生成 
    for(int i = 0; i < n; i++)//每次循环选出一个点加入到生成树
    {
        int t = -1;
        for(int j = 1; j <= n; j++)//每个节点一次判断
        {
            if(!st[j] && (t == -1 || dt[j] < dt[t]))//如果没有在树中，且到树的距离最短，则选择该点
                t = j;
        }

        //2022.6.1 发现测试用例加强后，需要判断孤立点了
        //如果孤立点，直返输出不能，然后退出
        if(dt[t] == 0x3f3f3f3f) {
            cout << "impossible";
            return;
        }


        st[t] = 1;// 选择该点
        res += dt[t];
        for(int i = 1; i <= n; i++)//更新生成树外的点到生成树的距离
        {
            if(dt[i] > g[t][i] && !st[i])//从 t 到节点 i 的距离小于原来距离，则更新。
            {
                dt[i] = g[t][i];//更新距离
                pre[i] = t;//从 t 到 i 的距离更短，i 的前驱变为 t.
            }
        }
    }

    cout << res;

}

void getPath()//输出各个边
{
    for(int i = n; i > 1; i--)//n 个节点，所以有 n-1 条边。

    {
        cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号，pre[i] 是 i 节点的前驱节点。他们构成一条边。
    }
}

int main()
{
    memset(g, 0x3f, sizeof(g));//各个点之间的距离初始化成很大的数
    cin >> n >> m;//输入节点数和边数
    while(m --)
    {
        int a, b, w;
        cin >> a >> b >> w;//输出边的两个顶点和权重
        g[a][b] = g[b][a] = min(g[a][b],w);//存储权重
    }

    prim();//求最下生成树
    //getPath();//输出路径
    return 0;
}


作者：Hasity
链接：https://www.acwing.com/solution/content/38312/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

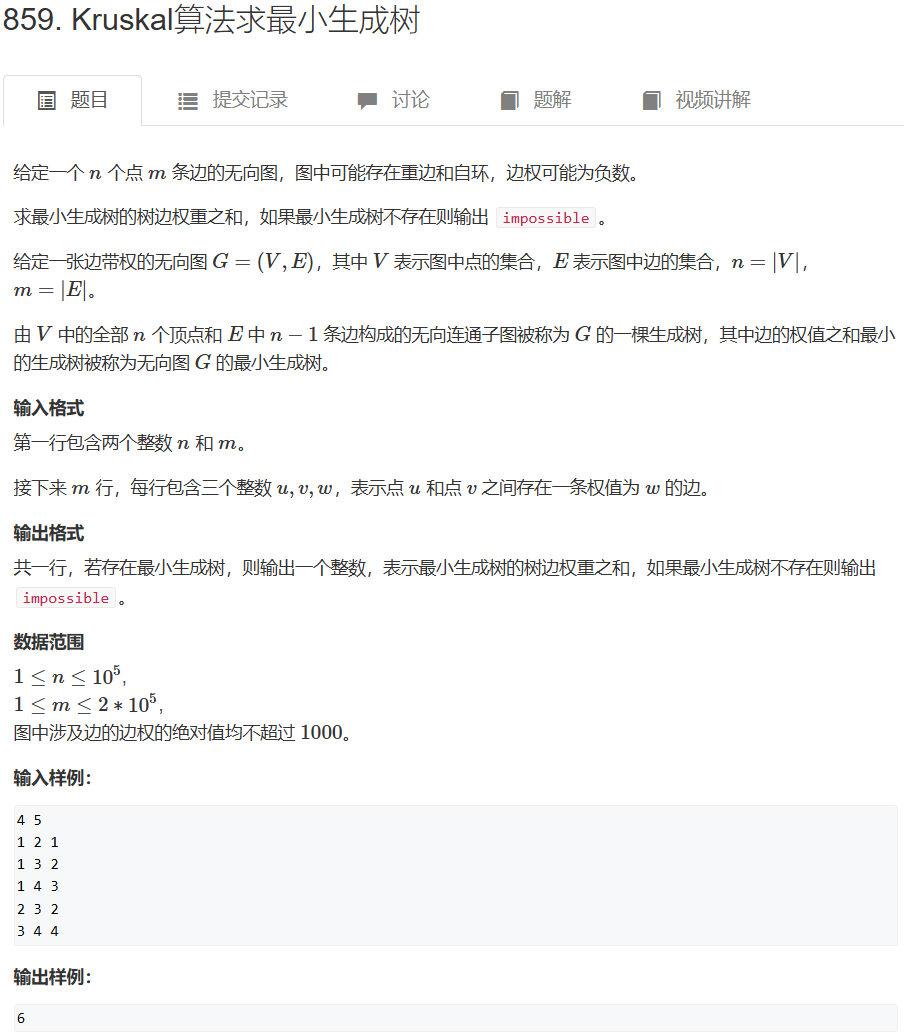
AcWing 859. Kruskal算法求最小生成树

kruskal算法：

通过并查集对边进行合并。先按照从小到大的权重进行排序，然后对每两个未连接的节点进行连边。我们知道，对于一个无向图，每两点有且仅有一条边相连，若其边数小于n-1，则其不联通，不能构成最小生成树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstring>
#include <algorithm>

using  namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge {
    int a, b, w;
    bool operator<(const Edge &E) const{
        return w < E.w;
    }
} edges[M];



int find(int x){        //并查集
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal(){
    sort(edges, edges + m);     
    for (int i = 1; i <= n; i ++ ) p[i] = i;    //初始化并查集
    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        if (a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }
    if (cnt < n - 1) return INF;        // 如果边的数量不足 n-1，说明图不连通
    else return res;
}


int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

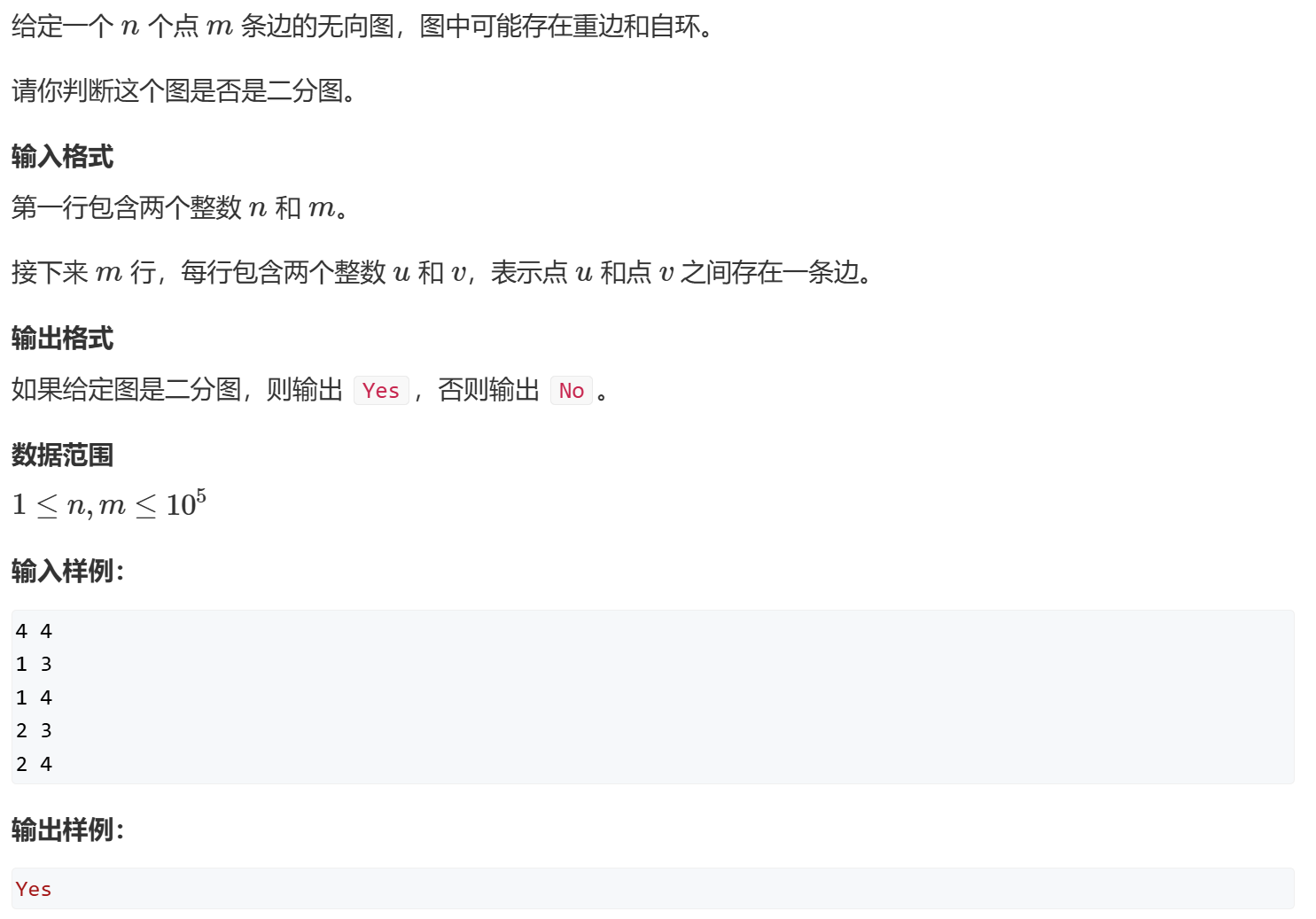
二分图

  • 染色法 O(n+m)
  • 匈牙利算法 O(mn)，实际运行时间很小
  • 二分图：二分图是一种特殊的图，其顶点集可以分成两个互不相交的子集，使得每一条边的两个端点分别属于不同的子集。（集合内部没有边）
  • 二部：如果一个图是二分图，那么它没有奇数长度的环。
  • 着色：一个图是二分图当且仅当它可以被 2着色，即可以使用两种颜色对图的顶点进行着色，使得每条边的两个端点的颜色不同。

染色法

AcWing 860. 染色法判定二分图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010 * 2;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int color[N];//保存各个点的颜色，0 未染色，1 是红色，2 是黑色
int n, m;//点和边

void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool dfs(int u, int c)
{
    color[u] = c;//u的点成 c 染色

    for(int i = h[u]; i!= -1; i = ne[i])
    {
        int b = e[i];                   
        if(!color[b])
        {
            if(!dfs(b, 3 - c)) return false;//（3 - 1 = 2， 如果 u 的颜色是2，则和 u 相邻的染成 1）
                                            //（3 - 2 = 1， 如果 u 的颜色是1，则和 u 相邻的染成 2）
        }
        else if(color[b] == c)//如果已经染色，判断颜色是否为  c
        {                                     
            return false;              
        }
    }
    return true;
}



int main(){
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i = 0;i < m; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }
     for(int i = 1; i <= n; i++)//遍历点
    {
        if(!color[i])//如果没染色
        {
            if(!dfs(i, 1))//染色该点，并递归处理和它相邻的点
            {
                cout << "No" << endl;
                return 0;
            }

        }
    }
    cout << "Yes" << endl;
    return 0;

}

匈牙利算法：

匈牙利算法是一种用于解决指派问题（Assignment Problem）的数学算法。指派问题是指在有限的候选者中选择一组匹配，使得总的成本最小（或收益最大）。

AcWing 861. 二分图的最大匹配

find(int u): 尝试为左边节点 u 找到一个匹配，使用递归方式实现深度优先搜索（DFS）。

如果右边节点 j 未被访问过，则标记为已访问。

如果右边节点 j 未匹配或者其匹配的左边节点可以重新匹配，则更新匹配关系并返回 true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstring>
using namespace std;

const int N = 505, M = 1e5 + 10;

int n1,n2, m;
int h[N], e[M], ne[M], idx;

int match[N], st[N];	//st标记右半部分


void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int find(int u) // 匈牙利算法
{
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            st[j] = true;      //标记该节被占用，后续调用不能使用该节点
            if(match[j] == 0 || find(match[j])){    //如果该节点没有被匹配，则匹配
                                                    //若该节点已匹配，则递归调用重新匹配节点
                match[j] = u;
                return true;
            }
        }
    }
    return false;
}

int main(){
    memset(h, -1, sizeof h);
    scanf("%d%d%d", &n1, &n2, &m);
    for(int i = 0; i < m; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);	// 保存图，因为只从一遍找另一边，所以该无向图只需要存储一个方向
    }
     int res = 0;
    //为各个点找匹配
    for(int i = 1; i <= n1; i++){
        memset(st, 0, sizeof st);   //将st数组置0，使得所有节点都没有被标记
        if(find(i)) res++;
    }
    cout << res;
    return 0;
}

提高课

  • 普通 BFS：从单个起点出发，逐层扩展。
  • 多源 BFS：从多个起点同时出发，逐层扩展。
    • 取一虚拟原点，将所有起点以边权为0连接到虚拟原点，则转化为单源BFS

多源BFS

AcWing 173. 矩阵距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <cstring>
#include <iostream>
#include <queue>
#include <utility>
using namespace std;
typedef long long LL;
const int N = 1e3 +10; 
int arr[N];
char g[N][N];
int d[N][N];


typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;
int xway[4] = {-1, 1, 0, 0};
int yway[4] = {0, 0, -1, 1};
void bfs()
{
    queue<pair<int, int>> qu;
    memset(d, -1, sizeof d);
    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
    {
        if(g[i][j] == '1')
        {
            qu.push({i, j});
            d[i][j] = 0;
    
       }
    }
    while(!qu.empty())
    {
        auto t = qu.front();
        qu.pop();
        for(int i = 0; i < 4; i++)
        {
            int x = t.first + xway[i];
            int y = t.second + yway[i];
            if(x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                qu.push({x, y});
            }
        }
    }
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n >> m;
    for(int i = 0 ; i < n ; i ++)
        cin>>g[i];
    bfs();
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << d[i][j] << ' ';
        }
        cout << "\n";
    }
}

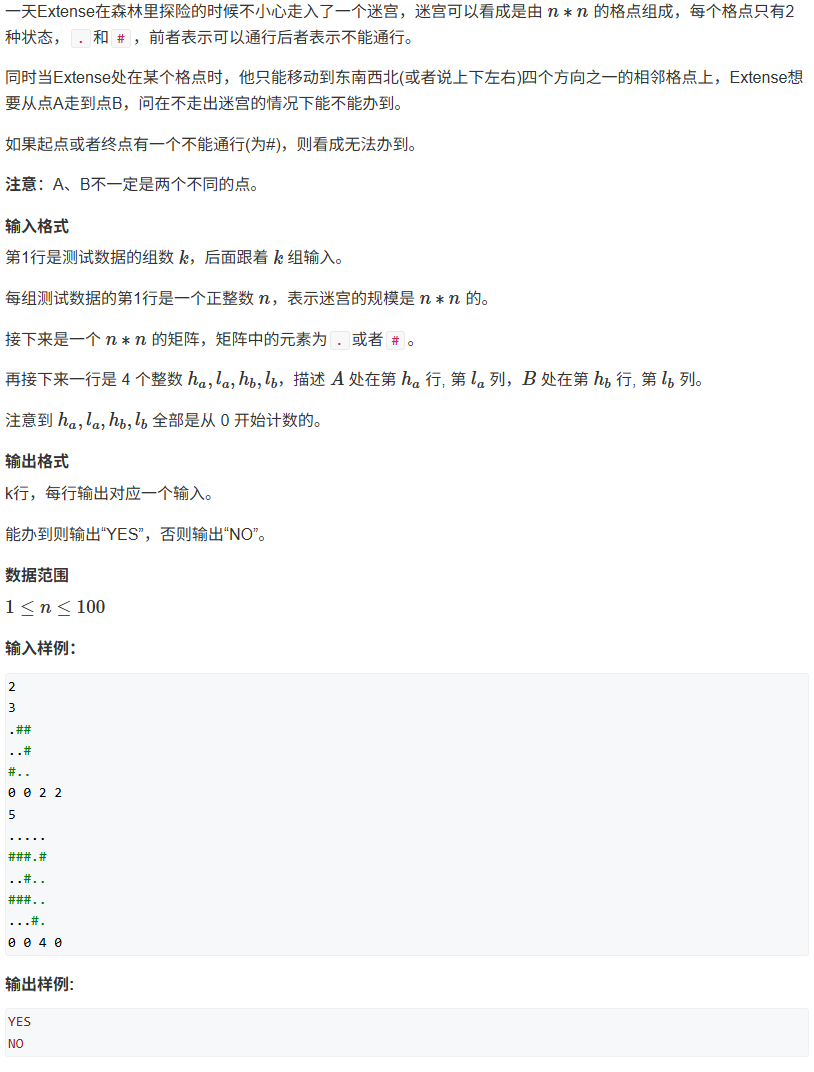
DFS之连通性模型

AcWing 1112. 迷宫

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <iostream>
#include <utility>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e3 +10; 
bool d[N][N];
bool st[N][N];

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;

int xway[4] = {-1, 1, 0, 0};
int yway[4] = {0, 0, -1, 1};
int sx,sy,ex,ey;



bool dfs(int x, int y) {	
    if(x==ex && y==ey)      	//判断终点
        return true;
    st[x][y] = true;
    for(int i = 0; i < 4; i++)
    {
        int nx = x + xway[i];
        int ny = y + yway[i];
        if(nx>=1 && ny>=1 && nx<=m && ny<=m && !st[nx][ny] && d[nx][ny]!=1)
        {
            if(dfs(nx,ny)) return true;     //直接返回到solve
        }
    }
    return false;
}

void solve() {
    cin >> m;
    for(int i = 1; i <= m; i++)
     for(int j = 1; j <= m; j++)
    {
        char ch;
        cin >> ch;
        if(ch=='#') d[i][j] = true;
        else d[i][j] = false;
    }
    memset(st,false,sizeof st);
    cin >> sx >> sy >> ex >> ey;
    sx++;
    sy++;
    ey++;
    ex++;
    if(d[sx][sy] || d[ex][ey])
    {
        cout << "NO" << endl;    //特判
    }
    else {
        if(dfs(sx,sy)) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n;
    while(n--) {
       solve();
    }
}

AcWing 1113. 红与黑

BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <iostream>
#include <utility>
#include <queue>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e3 +10; 
bool arr[N][N];
bool st[N][N];

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;

int sx,sy;

int dx[] = {-1,0,0,1};
int dy[] = {0,-1,1,0};
int BFS()
{
    int res =1;
    queue<PA> q;
    st[sx][sy] = true;
    q.push({sx,sy});

    while(q.size())
    {
        auto tmp = q.front();
        sx = tmp.first;
        sy = tmp.second;
        q.pop();
        for(int i = 0;i < 4;i++)
        {
            
            int xx = sx + dx[i];
            int yy = sy + dy[i];
            if(xx < 1 || xx> m || yy < 1 || yy > n)
            {
                //cout << xx << " " << yy << endl;
                //cout << endl;
                continue;
            }
                
            if(arr[xx][yy] && !st[xx][yy])
            {
                q.push({xx,yy});
                
                res++;
                //cout << 2323<<endl;
                st[xx][yy] = true;
    
            }
        }
    }
   
    return res;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    while(1)
    {
        memset(st,0,sizeof st);
        cin >> n >> m;
        if(n==0 && m==0)    return 0;
        for(int i = 1;i <= m;i++)
        {
            for(int j = 1;j <= n;j++)
            {
                 char tmp;
                 cin >> tmp;
                 if(tmp == '.')
                    arr[i][j] = true;
                 else if(tmp == '@')
                    {
                        sx = i;
                        sy = j;
                        arr[i][j] = true;
                    }
                 else
                 {
                    arr[i][j] = false;
                    
                 }
          //      cout << arr[i][j] << " ";            
            }
       //     cout << endl;
        }
       
        cout << BFS() << endl;
        
       
    }
}

DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <iostream>
#include <utility>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e3 +10; 
bool arr[N][N];
bool st[N][N];

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;
int sx,sy;


int dx[] = {-1,0,0,1};
int dy[] = {0,-1,1,0};

int dfs(int x, int y)
{
    int res = 0;
    st[x][y] = true;
    for(int i = 0; i<4;i++)
    {
        int xx = x + dx[i];
        int yy = y + dy[i];
        if(xx < 1 || xx > m || yy < 1 || yy > n)
            continue;
        if(arr[xx][yy] && !st[xx][yy])
        {
            res+=  dfs(xx,yy);
        }
    }
    return res + 1;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    while(1)
    {
        memset(st,0,sizeof st);
        cin >> n >> m;
        if(n == 0 && m == 0)
            break;
        for(int i = 1; i<=m;i++)
            for(int j = 1; j<=n;j++)
        {
            char tmp;
            cin >> tmp;
            if(tmp == '.')
               arr[i][j] = true;
            else if(tmp == '@')
               {
                   sx = i;
                   sy = j;
                   arr[i][j] = true;
               }
            else
            {
               arr[i][j] = false;
            }
          
        }
        
        cout << dfs(sx,sy) << endl;
    }

}

DFS之搜索顺序

AcWing 1116. 马走日

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10;
int t,n,m,sx,sy,ans = 0;
int dx[] = {1,-1,2,-2,1,-1,2,-2};
int dy[] = {2,2,1,1,-2,-2,-1,-1};
bool vis[N][N];
void dfs (int x,int y,int t) {
    if (t == n * m) {
        ans++;
        return ;
    }
    for (int i = 0;i < 8;i++) {
        int a = x + dx[i],b = y + dy[i];
        if (a < 0 || a >= n || b < 0 || b >= m || vis[a][b]) continue;
        vis[a][b] = true;
        dfs (a,b,t + 1);
        vis[a][b] = false;
    }
}
int main () {
    cin >> t;
    while (t--) {
        ans = 0;
        memset (vis,false,sizeof (vis));
        cin >> n >> m >> sx >> sy;
        
        vis[sx][sy] = true;
        dfs (sx,sy,1);
        cout << ans << endl;
    }
    return 0;
}

AcWing 1117. 单词接龙

预处理字符串，将所有拼接的可能转化可达数组g[N][N]==重复字符串长度，然后对图进行遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 21;

int n;
string word[N];
int g[N][N];
int used[N];
int ans;

void dfs(string dragon, int last)
{
    ans = max((int)dragon.size(), ans);
    used[last] ++ ;
    for (int i = 0; i < n; i ++ )
        if (g[last][i] && used[i] < 2)
            dfs(dragon + word[i].substr(g[last][i]), i);
    used[last] -- ;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> word[i];
    char start;
    cin >> start;

        // 预处理单词间重叠关系
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
        {
            string a = word[i], b = word[j];
            for (int k = 1; k < min(a.size(), b.size()); k ++ )
                if (a.substr(a.size() - k, k) == b.substr(0, k))
                {
                    g[i][j] = k;
                    break;
                }
        }

       // 从所有以start开头的单词开始搜索
    for (int i = 0; i < n; i ++ )
        if (word[i][0] == start)
            dfs(word[i], i);

    cout << ans << endl;

    return 0;
}


DFS之剪枝与优化

AcWing 165. 小猫爬山

这题可以使用记忆化搜索或者使用深搜暴搜

深搜暴搜

  • k >= res, return //剪枝，大于当前最优答案直接返回（后续更新不能使k减少）。
  • 优先考虑决策少的组合（递归深度小）——将猫从大到小排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 20; 
int ans = N; 
int cat[N]; 
int sum[N]; 
int n, m; 

void dfs(int u, int k) {
    if (k >= ans) return; // 剪枝：当前缆车数已不小于已知最小值
    if (u == n) { // 所有小猫已分配
        ans = k;    //k一定是小于等于ans的
        return;
    }
    for (int i = 0; i < k; i++) { // 尝试放入已有缆车
        if (sum[i] + cat[u] <= m) {
            sum[i] += cat[u];
            dfs(u + 1, k);
            sum[i] -= cat[u]; // 回溯
        }
    }
    // 新开一辆缆车
    sum[k] = cat[u];
    dfs(u + 1, k + 1);
    sum[k] = 0; // 回溯
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> cat[i];
    }
    sort(cat, cat + n, greater<int>()); // 从大到小排序
   //  sort(cat,cat+n);
  //  reverse(cat,cat+n);
    dfs(0, 0); // 初始调用：处理第0只小猫，当前缆车数为0
    cout << ans << endl;
    return 0;
}

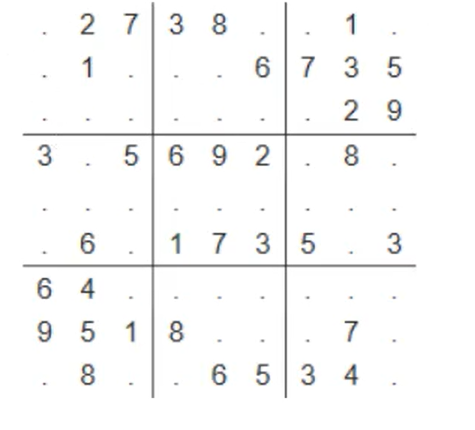
AcWing 166. 数独

要求：

  1. 每一行1-9
  2. 每一列1-9
  3. 九宫格1-9

优化：

  • 优化搜索顺序
    • 从当前能填合法数字最少的位置开始填数字
    • 使用ones存储数字i的二进制1的个数
    • 使用map存储可以当前二进制对应的数字·
  • 排除等效冗余
    • 任意一个状态下,我们只需要找一个位置填数即可,而不是找所有的位置和可填的数字.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include <cstring>
#include <iostream>

using namespace std;


const int N = 9, M = 1 << N;    // N=9（数独大小），M=512（2^9，所有可能的数字组合）

int ones[M];     // ones[i]：数字i的二进制1的个数
int map[M];     //map[i]：数字i对应的log2值，即可以选择的数字
int row[N], col[N], cell[3][3]; // 行、列、3×3宫的可用数字掩码
char str[100];


void init()
{
    for(int i = 0; i < N; i ++)
        row[i] = col[i] = (1 << N) - 1;  //  初始所有数字可用（二进制全1）

    for(int i = 0; i < 3; i ++)
        for(int j = 0; j < 3; j ++)
            cell[i][j] = (1 << N) - 1;   // 3×3宫初始所有数字可用
}

inline int lowbit(int x)    // 返回 x 的二进制最低位的 1
{
    return x & (-x);
}

int get(int x, int y)       // 返回 (x,y) 可用的数字掩码
{
    return row[x] & col[y] & cell[x / 3][y / 3];
}

void draw(int x, int y, int t, bool is_set)     // x,y为当前位置，t为当前数字，is_set为是填入还是删除
{
    if(is_set)  str[x * N + y] = t + '1';
    else str[x * N + y] = '.';

    int v = 1 << t;
    if(!is_set) v = -v;

    row[x] -= v;
    col[y] -= v;
    cell[x / 3][y / 3] -= v;
}

bool dfs(int cnt)
{
    if(!cnt)    return true;        // 填入所有数字后，成功

    // 找可填数字最少的空格（优化搜索顺序）
    int x, y;
    int minv = 10;
    for(int i = 0; i < N; i ++)
        for(int j = 0; j < N; j ++)
            if(str[i * N + j] == '.')
            {
                int state = get(i,j);
                if(ones[state] < minv)
                {
                    minv = ones[state];
                    x = i, y = j;
                }
            }

    // 尝试所有可填数字
    int state = get(x, y);
    for(int i = state; i; i -= lowbit(i))
    {
        int t = map[lowbit(i)];      // 取出最低位的 1 对应的数字
        draw(x, y, t, true);
        if(dfs(cnt - 1)) return true;   // 若成功直接回溯到main函数
        draw(x, y, t, false);
    }
    return false;
}


int main()
{
    for(int i = 0; i< N; i ++)
       map[1 << i] = i;    // 将1 << i映射到i
    for(int i = 0; i < 1<< N; i ++)
        for(int j = 0; j < N; j ++)
            ones[i] += (i >> j) & 1;    // 计算i的二进制中1的个数

    while(cin >> str, str[0] != 'e')
    {
        // i是行号，j是列号，k是str索引
        init();
        int cnt = 0;    // 统计空格数量
        for(int i = 0, k = 0; i < N; i ++)
            for(int j = 0; j< N; j++, k++)
                if (str[k] != '.')
                  {
                    int t = str[k] - '1';
                    draw(i,j,t,true);
                  }
                else
                    cnt ++;
        dfs(cnt);
        puts(str);
    }
    return 0;
}