A

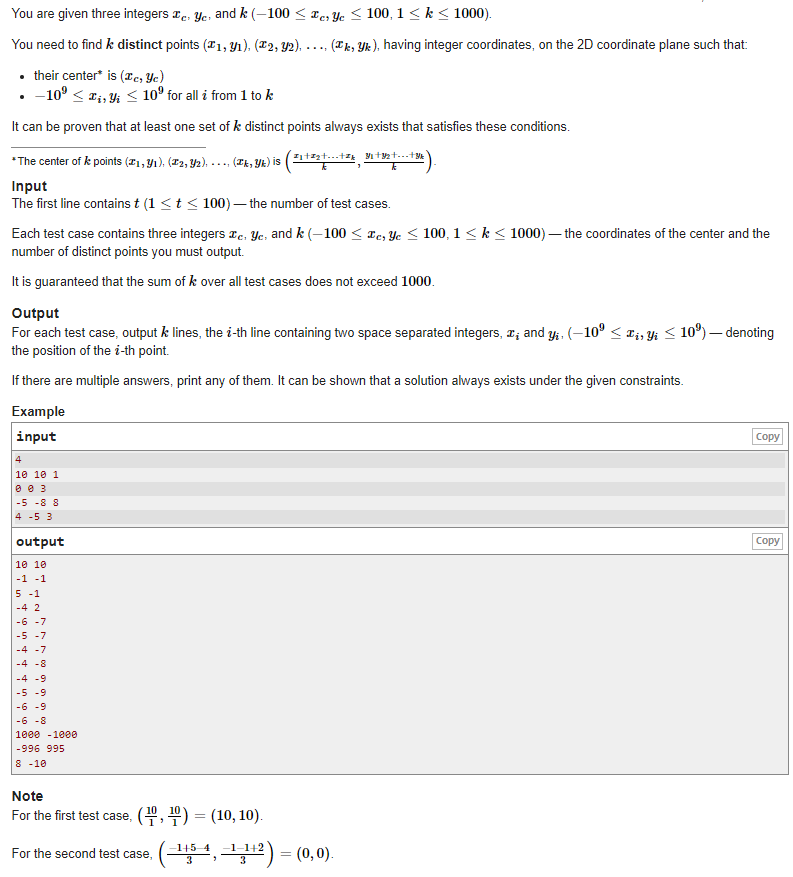
题意你需要在二维平面上找到 k 个不同的整数坐标点$ (x1,y1)(x_1, y_1)(x1,y1), (x2,y2)(x_2, y_2)(x2,y2), …, (xk,yk)(x_k, y_k)(xk,yk)$，使得这些点的中心（质心）是给定的点$ (xc,yc)(x_c, y_c)(xc,yc)$。

  • 对于偶数个，使得输出值平均分配在输入两侧

  • 对于奇数个，同时输出中间值（即输入）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>

using namespace std;

typedef long long LL;                            

void solve() {
    int a, b, c;
    cin >> a >> b >> c;
    int cnt = c / 2;

    for(int i = 1; i <= cnt; i++) {
        cout << a - i << " " << b - i << endl;
        cout << a + i << " " << b + i << endl;
    }

    if(c % 2 != 0) {
        cout << a << " " << b << endl; 
    }
}

int main() {
    int n;
    cin >> n;
    while(n--) {
       solve();
    }
}

B

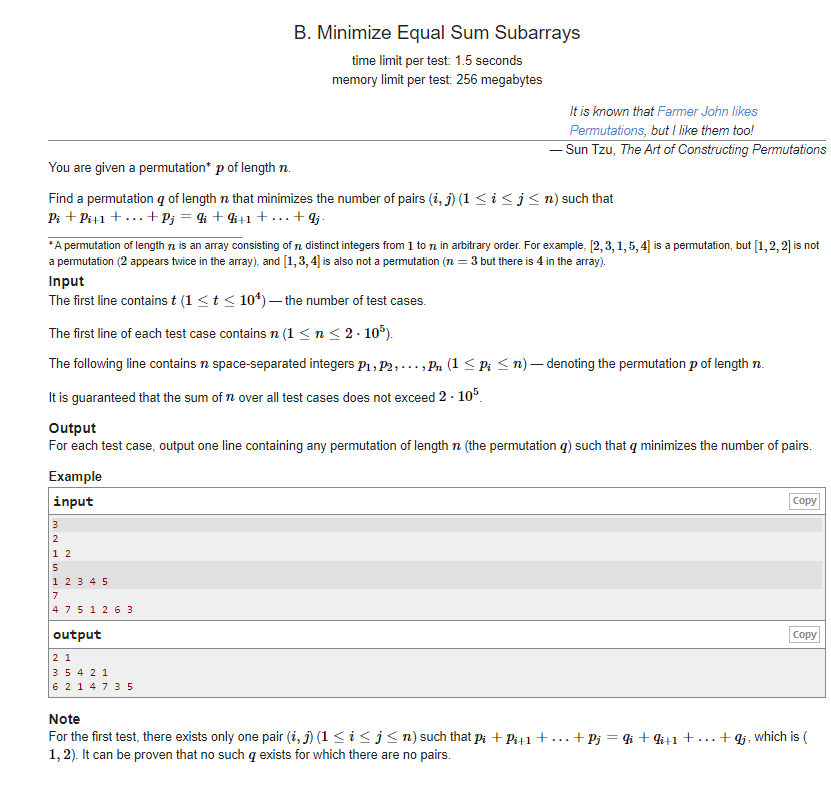
题意：你需要找到一个新的排列 q，使得其子数组的所有可能的和，与 p 的子数组的和相等的情况尽量少。

Codeforces Round 965 (Div. 2) 题解 - definieren - 博客园 (cnblogs.com)

先猜只有 [1,n][1,n] 的和相等。
做前缀和，问题就变成了$ sumpr−sumpl≠sumqr−sumqlsumpr−sumpl≠sumqr−sumql$。
移项可得 $sumpr−sumqr≠sumpl−sumplsumpr−sumqr≠sumpl−sumpl$。
这就是在说，对于$ i≠ni≠n，Δi=sumqi−sumpiΔi=sumqi−sumpi $互不相等。

然后枚举构造方式，发现可以构造 $qi=pimodn+1qi=pimodn+1$。
不难发现，如果$ pi<npi<n$，则 $Δi=Δi−1+1Δi=Δi−1+1$；如果$ pi=npi=n$，则 $Δi=Δi−1−(n−1)Δi=Δi−1−(n−1)$。
观察到只有 $Δ0=Δn=0Δ0=Δn=0$，所以这个构造是对的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <iostream>

using namespace std;

typedef long long LL;
const int N = 2e6 + 10;
int q[N], p[N];
void solve() {
  int n;
  cin >> n;

  for (int i = 0; i < n; ++i) {
    cin >> p[i];
  }
  for (int i = 0; i < n; i++) {
    q[i] = p[(i + 1) % n];
  }
  for (int i = 0; i < n; ++i) {
    cout << q[i] << " ";
  }
  cout << endl;
}

int main() {
  int n;
  cin >> n;
  while (n--) {
    solve();
  }
}