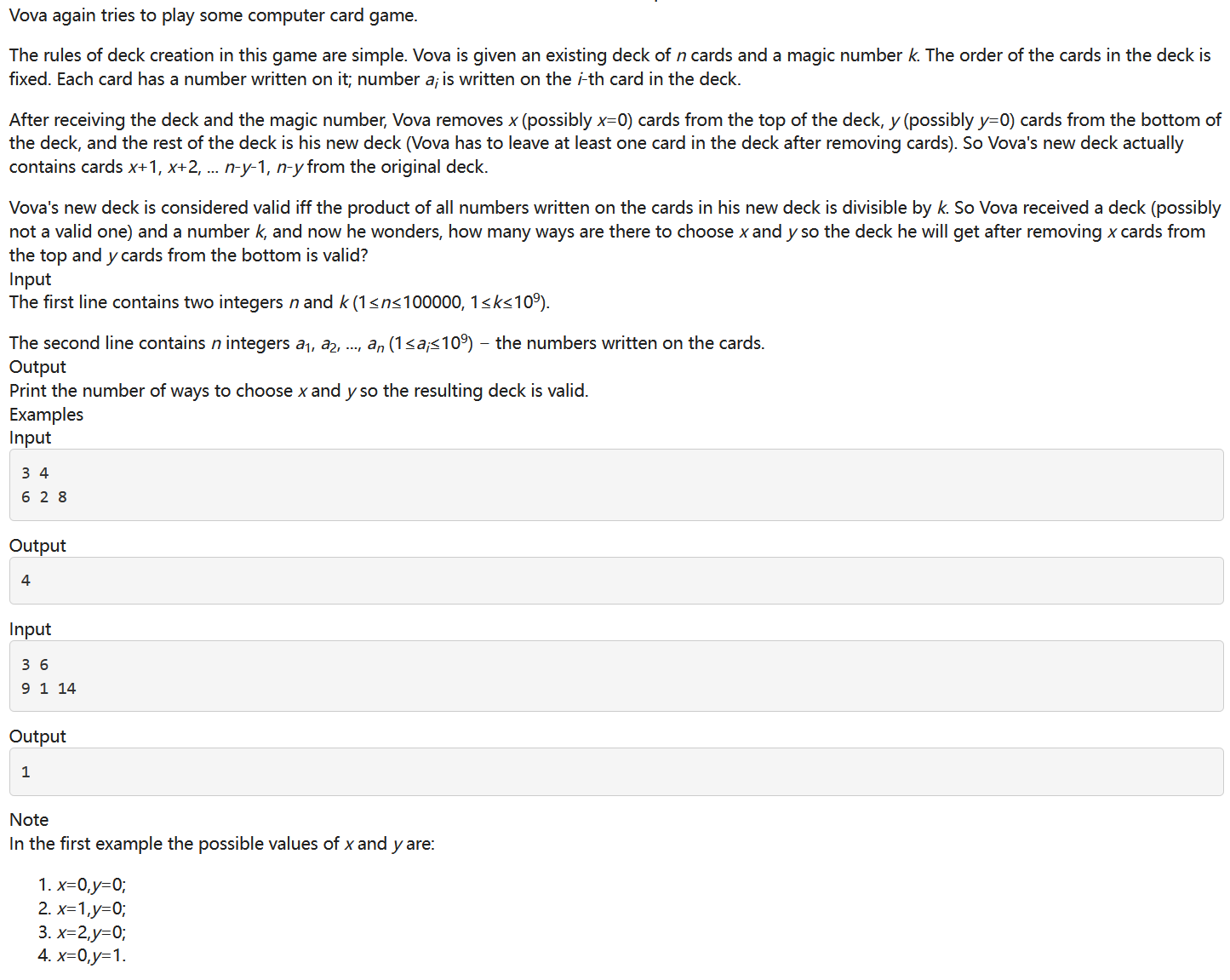
A :Card Game Again

0x1 滑动窗口(推公式)

这题的关键在于区间公式的推导

  1. 一旦某个子数组 [l, r] 的乘积能被 k 整除，那么所有包含 [l, r] 的子数组（即 [a, b] 满足 a ≤ l 且 b ≥ r）也一定满足条件。因为 k 已经是 [l, r] 的因数，再乘任何数不会改变整除性。
  2. 找到最小的 [l, r] 满足条件后，所有 [a, b]（a ≤ l 且 b ≥ r）都满足条件。
  3. 考虑多个区间，若第一个区间已经被计算过，则计算第二个区间时，第一个区间左边界已经被就是你过，因此计算使用第一个区间的左边界和第二个区间的右边界。
  4. (l - last_valid_l) * (n - r); 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
using namespace std;

const int N = 100000 + 10;  
int arr[N];

int main() {
    int n, m;
    cin >> n >> m;  // 输入数组长度n和除数m
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }

    int ans = 0;
    int l = 0, r = 0;
    int last_valid_l = -1;  // 上一个满足条件的左边界

    while (r < n) {
        // 1. 找到最小的r，使得arr[l..r]的乘积能被m整除
        long long product = 1;
        for (r = l; r < n; r++) {
            product = (product * arr[r]) % m;
            if (product == 0) {
                break;  // 找到右边界
            }
        }
        if (r == n) break;  // 无法找到满足条件的r，退出

        // 2. 找到最大的l，使得arr[l..r]的乘积能被m整除
        product = 1;
        for (l = r; l >= 0; l--) {
            product = (product * arr[l]) % m;
            if (product == 0) {
                break;  // 找到左边界
            }
        }

        // 3. 计算新增的满足条件的子数组数量
        ans += (l - last_valid_l) * (n - r);
        last_valid_l = l;  // 更新上一个满足条件的左边界

        // 4. 移动窗口
        l++;
        r++;
    }

    cout << ans << endl;
    return 0;
}

0x2暴力枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    int arr[n];
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }

    int ans = 0;
    for (int l = 0; l < n; l++) {
        long long product = 1;
        for (int r = l; r < n; r++) {
            product = (product * arr[r]) % m;
            if (product == 0) {
                ans += n - r;  // 所有以l开头，r到n-1结尾的子数组都满足
                break;
            }
        }
    }

    cout << ans << endl;
    return 0;
}

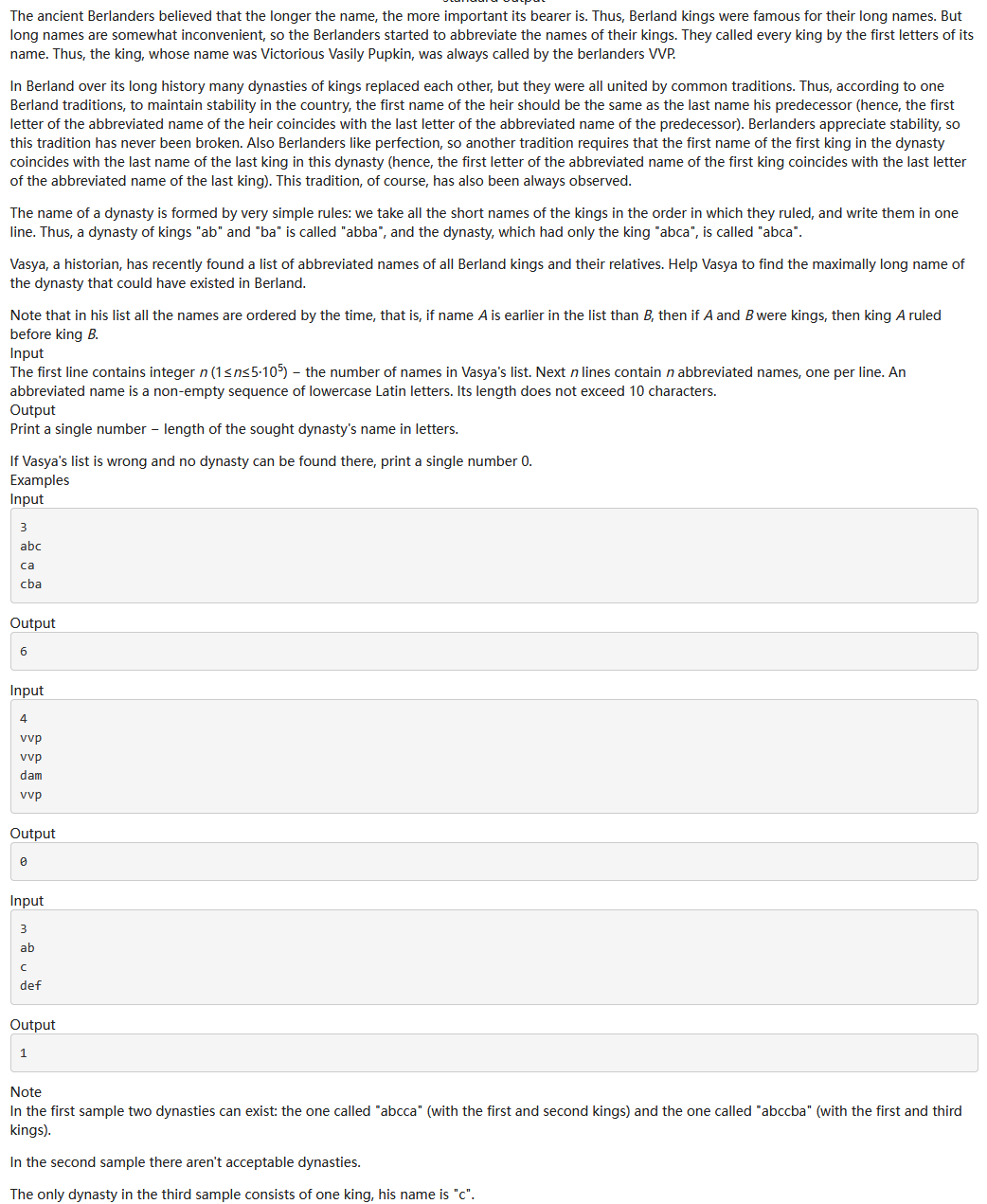
B:Dynasty Puzzles

这题在于读懂题意，按输入排序，若前面字符串结尾与后面字符串开头相同，则两个字符串可以拼接。

则可以用dp解决

dp[i][j]表示以i开头，j结尾的字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
char s[500010][15];
int f[26][26];
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <=n;i++)
    {
        cin >> s[i];
    }

    for(int i = 1; i<=n; i++)
    {
        int len = strlen(s[i]);
        int a = s[i][0] - 'a';
        int b = s[i][len - 1] - 'a';
        for(int j = 0; j < 26; j++)
           if(f[j][a])  f[j][b] = max(f[j][b],f[j][a]+len);
        f[a][b] = max(f[a][b],len);
    }
    int ans = 0;
    for(int i=0;i<26;++i)ans=max(f[i][i],ans);
	cout << ans << endl;
	return 0;
}

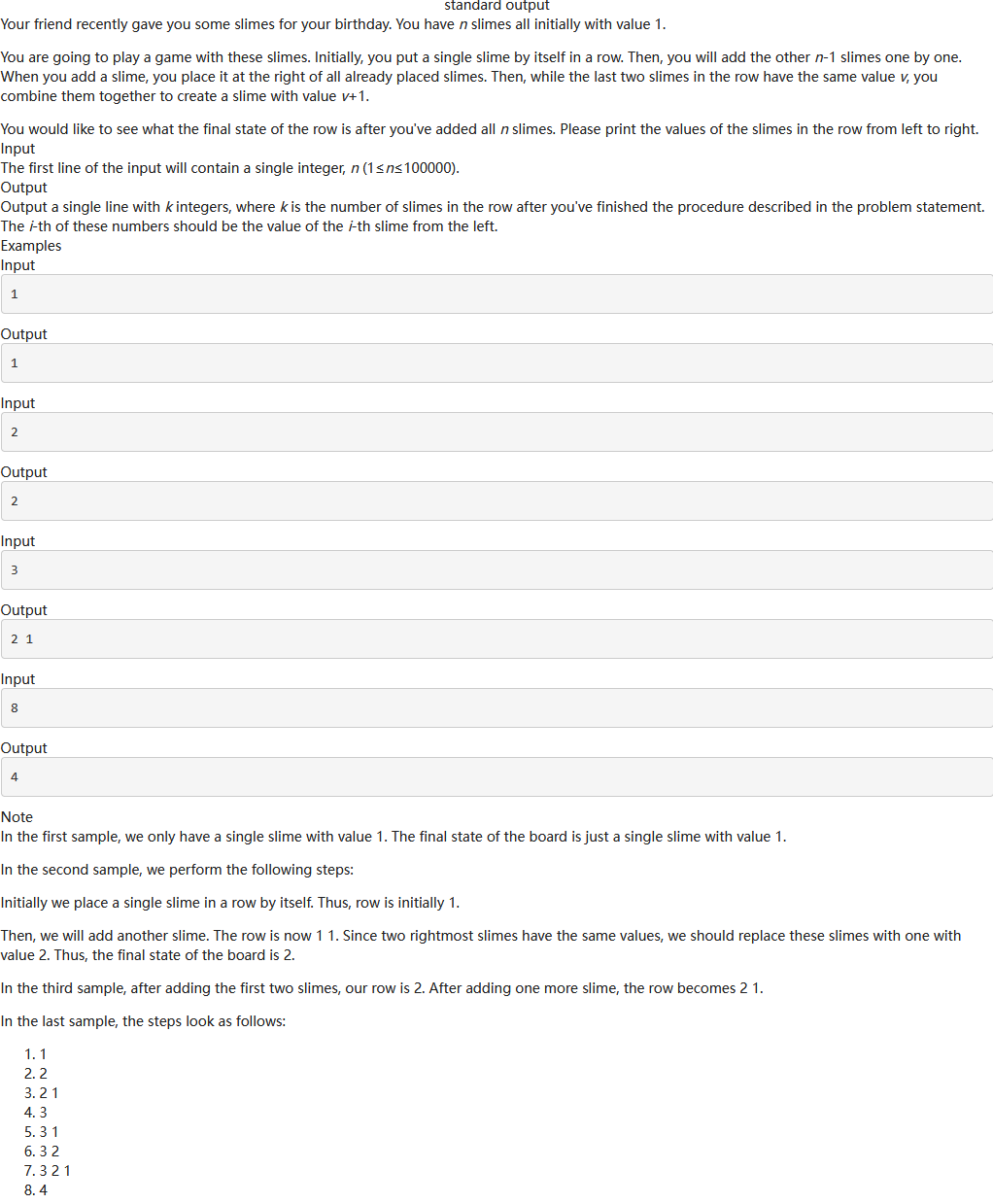
H:Slime Combining （二进制）

签到题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <utility>
#include <stack>
using namespace std;
typedef long long LL;
const int N = 1e5 +10; 
int arr[N];

typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;


stack<int> st;


int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n;
    while(n--)
    {
        st.push(1);
        while(st.size()>=2)
       {
        int a = st.top();
        st.pop();
        int b = st.top();
        st.pop();
        if(a==b)
            st.push(a+1);
        else
            {
                st.push(b);
                st.push(a);
                break;
            }
       }
    }
    int cnt = 0;
    while(!st.empty())
    {
        arr[cnt] = st.top();
        st.pop();
        cnt++;
    }
    for(int i = cnt-1; i>=0;i-- )
        cout << arr[i] << " ";
}