[toc]

A: Russian Roulette

题意翻译

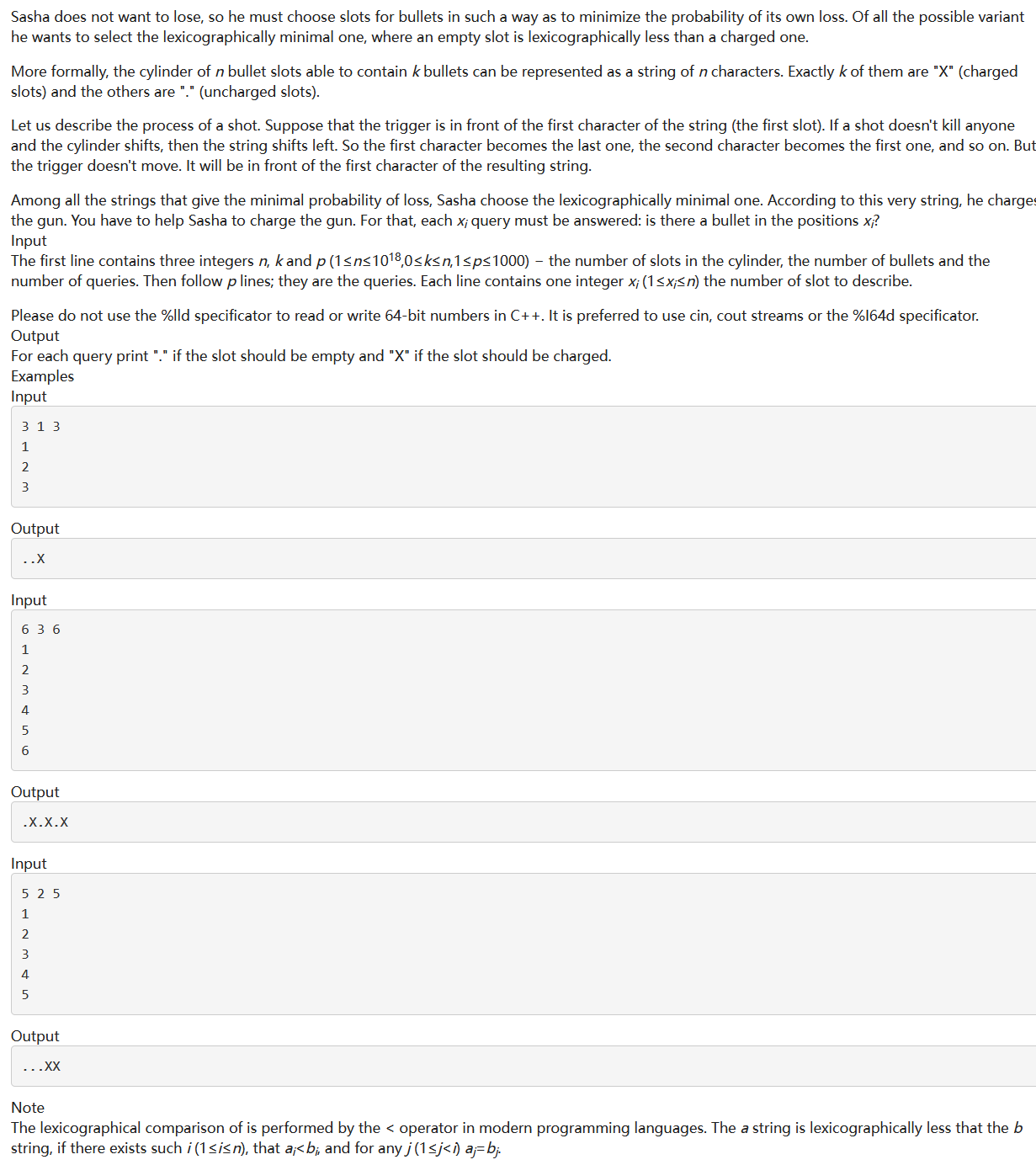
在Orlando发生了我们都知道的事情之后，Sasha和Roma决定找出谁仍然是球队最大的输家。谢天谢地，Masha在某个地方发现了一把左轮手枪，它的转轮上有n个弹槽，恰好可以装k个子弹，现在男孩们有机会一劳永逸地解决这个问题。

Sasha从n个弹槽中选择任意k个，然后把子弹放在那里。Roma旋转转轮，使得转轮的n种位置都是等概率的。然后游戏开始，玩家轮流操作，Sasha先手：他把枪顶着脑袋开枪。如果扳机前没有子弹，转轮会移动一个位置，手枪也会交给Roma，让Roma做出同样的动作。游戏一直持续到有人中枪，幸存者就是赢家。

Sasha不想输，所以他必须选择子弹放置的位置，这样才能把自己输的概率降到最低。

更正式地说，能够包含k子弹的n弹槽的圆柱体可以表示为n字符的字符串。其中k个是“X”（有子弹），其他是“.”（空弹槽）。定义“.”字典序小于“X”，在所有可能的方案中，他希望选择字典序最小的一个。

现在给出p个询问，要求你回答弹槽x是否有子弹。

题解(python)

情况可分为两种

  • 我们需要尽可能让先手赢，因此要尽量使得子弹间隔排列。

  • 对于偶数

    • 若子弹数量k*2小于蛋槽数，则排列在偶数位置，从后往前排列使得字典序最小
    • 若子弹数量k*2大于蛋槽数，则偶数位置都为子弹，奇数位置从后往前枚举使得字典序最小
  • 对于奇数
    • 如例三，可以证明...xx和..x.x先手获胜几率都为2/5，选择字典序最大的...xx，若至少有一颗子弹，我们特判最后位置询问，然后将奇数蛋槽转化为偶数蛋槽
  • 特判没有子弹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
n,k,m = map(int,input().split())

if k ==0:
    for i in range(n):
        print('.',end = '')
        exit(0)
if n%2==1:  #
    n-=1
    k-=1

pos2 = n+10 
pos1 = n+10
if n >= k*2:
    pos1 = n-k*2 + 2
else:
    pos1 = 2
    pos2 = n-(k-n/2)*2+1


for i in range(m):

    tmp = int(input())
    if tmp == n+1:  
        print('X',end='')
        continue
    if tmp%2==0:
        if tmp >= pos1:
            print('X',end='')
        else:
            print('.',end='')
    else:
        if tmp >= pos2:
            print('X',end='')
        else:
            print('.',end='')
# print()
# print()
# print(n)
# print(k)
# print(pos1)
# print(pos2)

B: Lucky Country （并查集+分组背包）

题意翻译

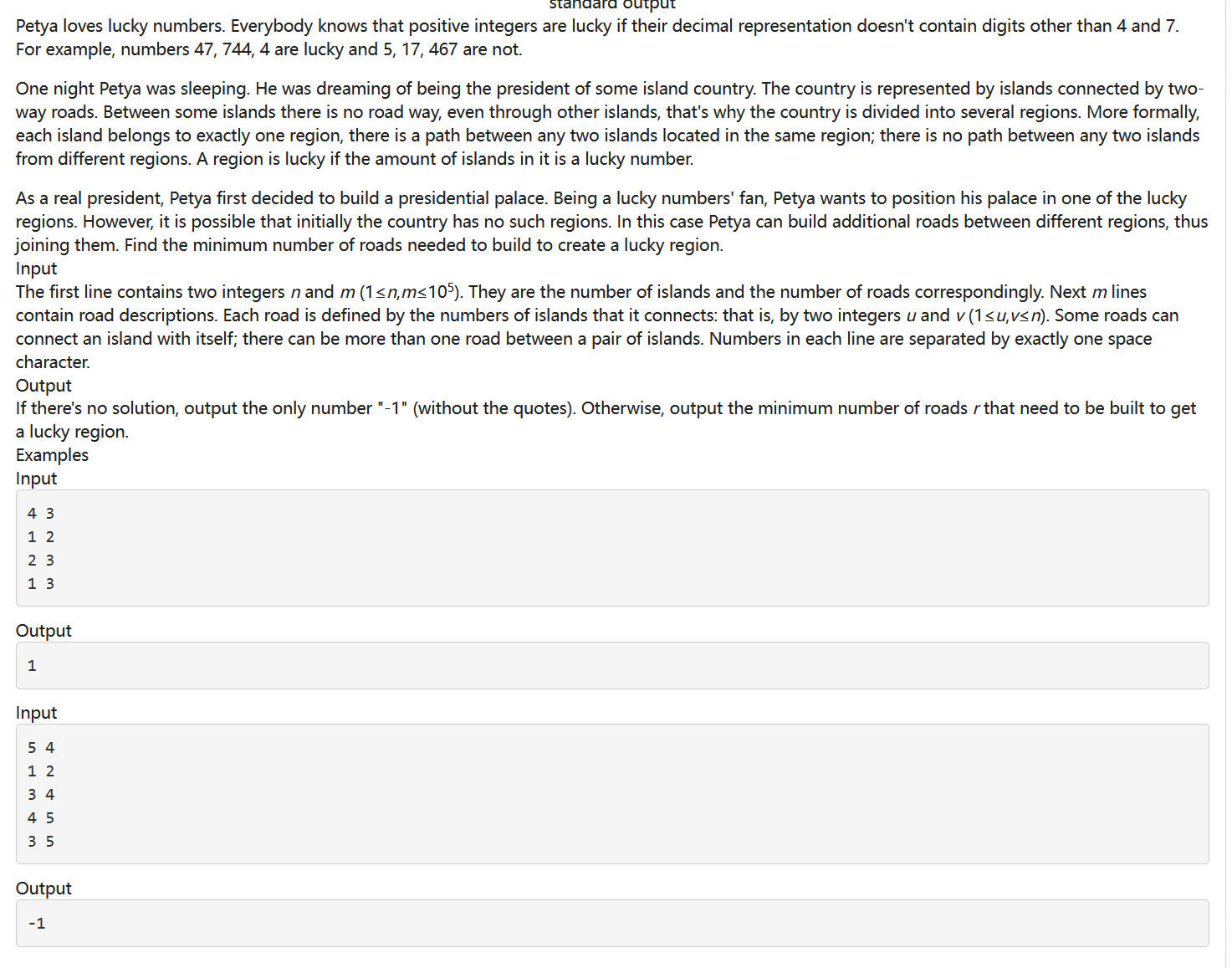
如果一个数中不包含除 4 和 7 之外的数字则是幸运数。有 n 个岛屿，通过双向道路连接。这些岛屿被分为几个地区。每个岛属于恰好一个区域，同一区域中的任何两个岛之间存在道路，不同区域的任何两个岛之间没有路径。如果一个地区的岛屿数量是一个幸运数字，则这个地区是幸运的。问最少增加几条道路能创建一个幸运地区。

超时做法

  • 通过dfs()对岛屿进行连接，统计连通块的数量
  • 通过dfs2()统计多个岛屿连接的所需的次数和值，更新arr数组为到达当前数字的最小值，最后输出下标为幸运数字的arr数组。
  • 算法瓶颈在于dfs()耗时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <cstring>
#include <iostream>
#include <utility>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 2e5 +10; 
int arr[N] ;
typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;

int h[N], ne[N],e[N],idx;

int point[N];
int pcnt = 0;

bool st1[N] = {false};
bool st2[N] = {false};

int brr[62]={4,7,44,47,74,77,444,447,474,477,744,747,774,777,4444,4447,4474,4477,4744,4747,4774,4777,7444,7447,7474,7477,7744,
    7747,7774,7777,44444,44447,44474,44477,44744,44747,44774,44777,47444,47447,47474,47477,47744,47747,47774,47777,
    74444,74447,74474,74477,74744,74747,74774,74777,77444,77447,77474,77477,77744,77747,77774,77777};

void add(int a, int b)
{
    e[idx]  = b;
    ne[idx] = h[a];
    h[a] = idx++;
}


void dfs2(int sum,int x)
{
   // cout << sum << " " << x << endl;
    arr[sum] = min(arr[sum],x);
  
  //  cout << sum <<  arr[sum] << " ";
    for(int i = 0; i < pcnt; i++)
    {
        if(!st2[i])
        {
            st2[i] = true;
            dfs2(point[i]+sum,x+1);
            
            st2[i] = false;
        }
    }
    
}
int dfs(int x)
{
    int sum = 1;
    st1[x] = true;
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
       
        if(!st1[j])
        {
            int s = dfs(j);
            sum += s;
        }
        
    }
    return sum;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    memset(h, -1, sizeof h);
    memset(arr, N, sizeof arr);
    cin.tie(0);			
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a,b);
        add(b,a);    
    }
    for(int i = 1; i <= n; i++)
    {
        if(!st1[i])
        {
            point[pcnt++] = dfs(i);
           // cout << i << " " << point[pcnt-1] << endl;
        }
    }
    // for(int i = 0; i < pcnt; i++)
    // {
    //     cout << point[i] << " ";
    // }
    
    
    dfs2(0,0);  //总和，步数
    int minnum = 1e9;
    for(int i = 0; brr[i] <= n ; i++)
    {
        if(arr[brr[i]] != 0 || arr[brr[i]]!=N)
        {
            //cout << brr[i] << " " << arr[brr[i]] << endl;
          //  cout << brr[i] << " " << arr[brr[i]] << endl;
                minnum = min(minnum,arr[brr[i]]);
        }
    }


    // for(int i = 0; arr[i] <= n ; i++)
    //     cout<< arr[i] << " ";

    if(minnum == 1e9)
    {
        cout << -1 << endl;
    }
    else
    {
        cout << minnum-1 << endl;
    }
    
}

并查集+多重背包：

  • 由于岛屿连接是无向的，我们可以使用并查集维护同一区域的点
  • 使用多重背包计算组合出”幸运数字”的最小操作数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include <iostream>
#include <utility>
#include <vector>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e5 +10; 
int p[N];
int siz[N];

int arr[N];
int v[N],w[N],s[N];
int f[N];



typedef pair<int, int> PA;
typedef pair<PA, int> PA2;
int n,m;



int find(int x){
    if(p[x]!=x)
    {
        p[x] = find(p[x]);
    }
    return p[x];
}

struct good{
    int w,v;
};


bool isLucky(int num) {
    if(num==0)  return false;
    while (num > 0) {
        int digit = num % 10;
        if (digit != 4 && digit != 7) return false;
        num /= 10;
    }
    return true;
}



int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);			
    cin >> n >> m;
    for(int i = 1; i <= n; i++)     //初始化并查集
       {
        p[i] = i;
        siz[i] = 1;
       }

    for(int i = 1 ; i <= m; i++)
    {
        int a,b;
        cin >> a >> b;
        if(find(a) == find(b)) continue;
        siz[find(a)] += siz[find(b)];
        p[find(b)] = find(a);
    }

    for(int i = 1; i <= n; i++)
    {
        if(find(i) == i)
            arr[siz[i]]++;
    }
    // for(int i = 1; i <= n; i++)
    // {
    //     cout << arr[i] << " ";
    // }
    memset(f, 0x3f, sizeof(f));  // 初始化为无穷大
    f[0] = 0;  // 背包容量为0时，总重量为0

    vector<good> Good;
    for(int i = 1; i <= n; i++)
    {
        if(arr[i])
        {
            int s = arr[i];
            for(int k = 1; k<=s; k*=2)
            {
                s-=k;
                Good.push_back({k,k*i});
            }
            if (s>0)    Good.push_back({s,s*i});
        }
        
    }
    //cout << Good.size() << endl;

    for(auto t: Good)
        {
          //  cout << t.w << " " << t.v << endl;
            for(int j = n; j >= t.v; j--)
            f[j] = min(f[j],f[j-t.v]+t.w);
        }
    
    int ans = 1e9;
    for (int i = 1; i <= n; i++) {
      // cout << f[i] << " "<< endl;
            if (f[i] != 0x3f3f3f3f) 
            {
                if(isLucky(i))
                    ans = min(ans,f[i]);
            }
    }
    if(ans == 1e9)
        ans = 0;
    cout << ans-1 << endl;
   
}

C: Friends

题意翻译

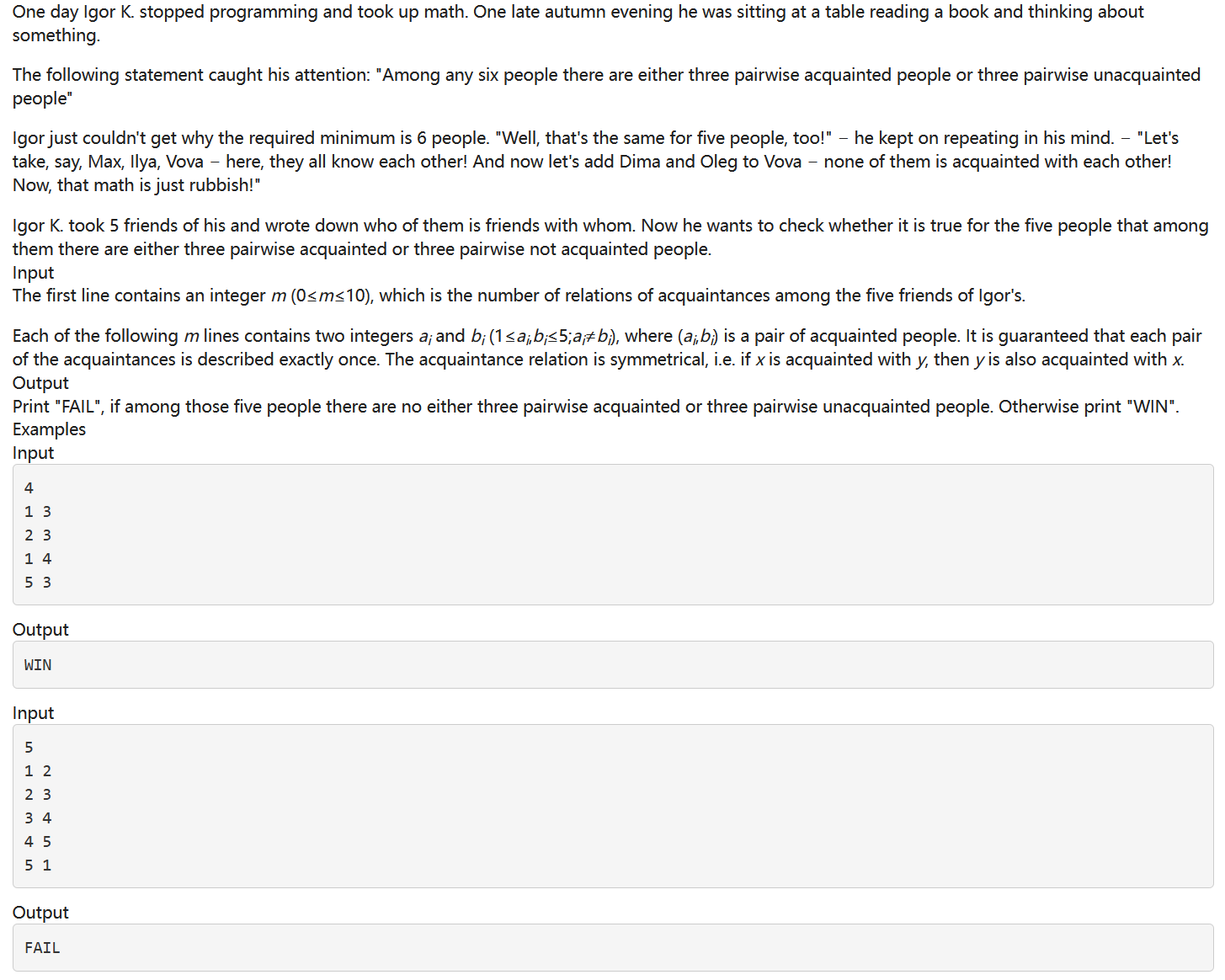
给定一个含 5 个点与 m 条线的无向图，求是否至少有 3 个点连通或不连通。

  • 如果是，输出 WIN；否则输出 FAIL。
  • 1≤m≤10，保证无重边与自环。

题解（python）

若全为度数为2的点，则输出FAIL

条件一：认识三对

条件二：三对不认识

  • 度数为 3：假设顶点 A 的度数为 3，即 A 与 B、C、D 相连。那么：

    • 如果 B、C、D 中有任意两个相连，则 A、B、C 或 A、B、D 或 A、C、D 形成一个三角形（三个互相认识的人）。

    • 如果 B、C、D 互不相连，则 B、C、D 形成一个独立集（三个互相不认识的人）。

  • 度数为 4：顶点 A 与四个其他顶点相连，剩下的一个顶点不与 A 相连。那么：

    • 四个相连的顶点中至少有三个互相认识或互相不认识（根据鸽巢原理）。
    • 如果不与 A 相连的顶点与其他顶点的连接情况也可能形成独立集。

  • 所有度数为 2 的情况：

    • 五个顶点，每个顶点度数为 2，意味着图中形成一个五边形（每个顶点与两个相邻顶点相连）。

    • 在这种情况下：

      • 无法找到三个互相认识的顶点（因为任何三个顶点中至少有一对不相连）。
      • 也无法找到三个互相不认识的顶点（因为任何三个顶点中至少有一对相连）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

arr = [[0]*10 for _ in range(10)]


n = int(input())

graph = {}

for i in range(n):
    x,y = map(int,input().split())
    if x not in graph:
        graph[x] = [y]
    else:
        graph[x].append(y)
    if y not in graph:
        graph[y] =[x]
    else:
        graph[y].append(x)

flag= False


for i in range(1,6):
    #print(len(graph[i]))
   
    if len(graph[i]) !=2:
        flag = True
if flag:
    print("WIN")
else:
    print("FAIL")

E: Vasya’s Function

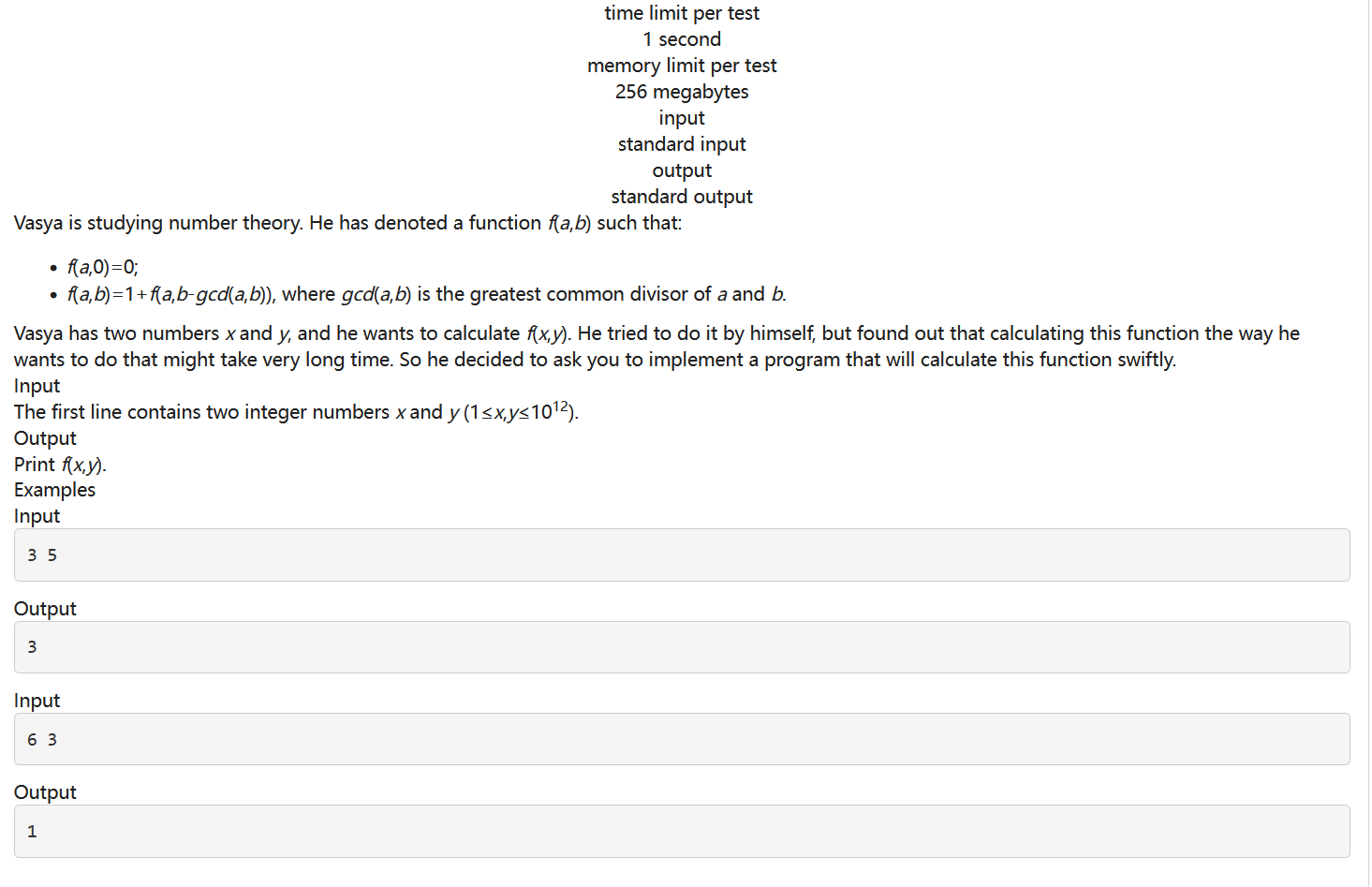
不会

F: Text Volume

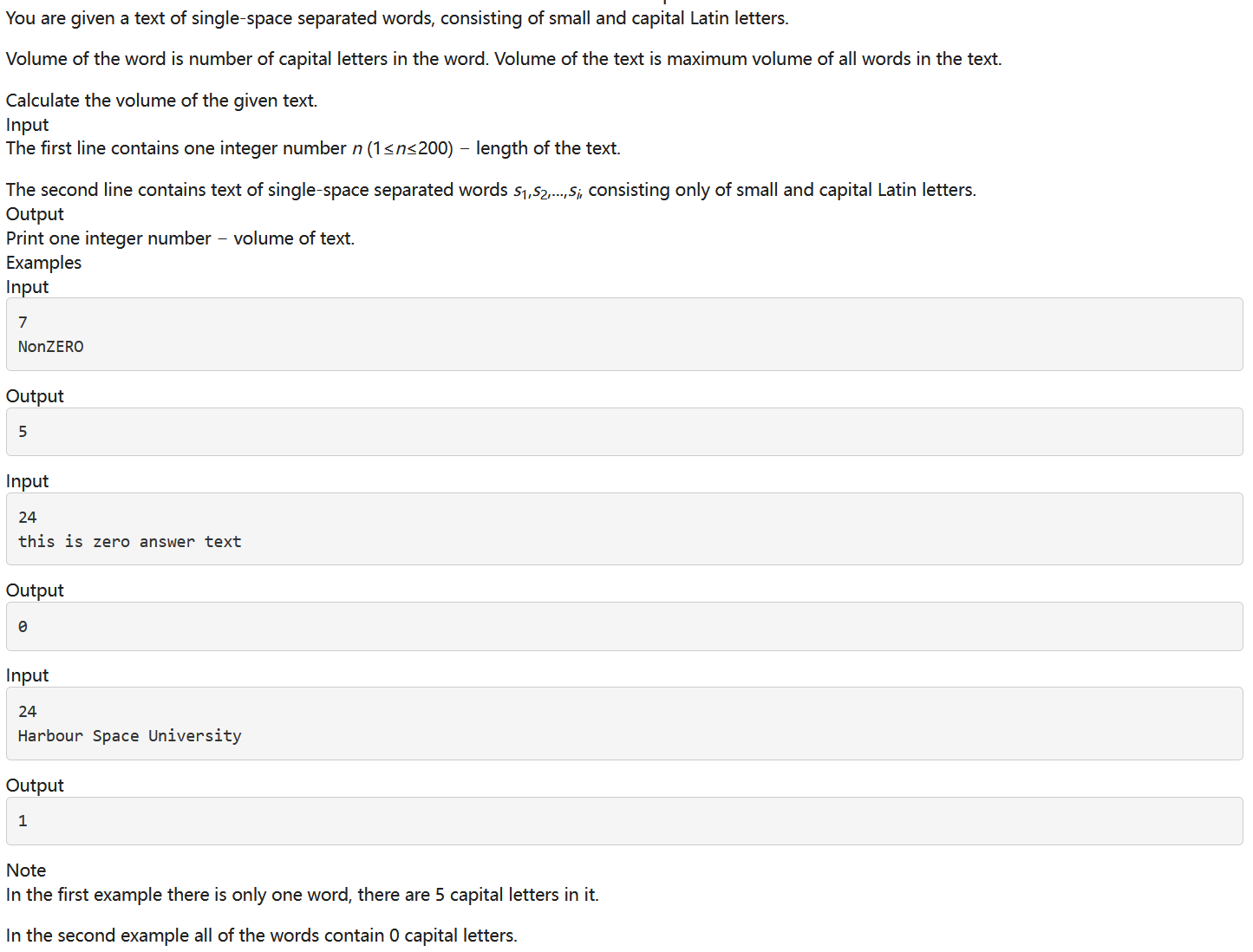
题意翻译

您将得到一个由单个空格分隔的单词组成的文本，其中包含小写字母和大写字母。计算单词中最多有多少个大写字母。

题解（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n = int(input())
s = input()
cnt = 0
maxnum = 0
for i in s:
    #print(i)
    if i == ' ':
        maxnum = max(maxnum, cnt)
        cnt = 0
        continue
    if i.isupper():
        cnt += 1

maxnum = max(maxnum, cnt)
print(maxnum)

G: Unimodal Array

题意

  • 判断一个数组是否符合”先严格递增，然后平稳（相等），最后严格递减”的模式
  • 一个数组也可以恒为常数

题解(python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
n = int(input())

arr = list(map(int,input().split()))
brr = [0] * (n+1)


flag1 = False
flag2 = False
flag3 = False

equnum = arr[0]
equ = True
for i in range(1,n):
    if equnum != arr[i]:
        equ = False
        break
if equ:
    print("YES")
    exit()


cnt = 1
for i in range(1,n):
    if arr[i] > arr[i-1]:
        cnt+=1
    else:
        break
flag1 = True

for i in range(cnt,n):
    if arr[i] ==  arr[i-1]:
        cnt+=1
    else:
        break
flag2 = True


for i in range(cnt,n):
    if arr[i] < arr[i-1]:
        cnt+=1
    else:
        break
    
flag3 = True

if flag1 and flag2 and flag3 and cnt == n:
    print("YES")
else:
    print("NO")

H:Okabe and Banana Trees

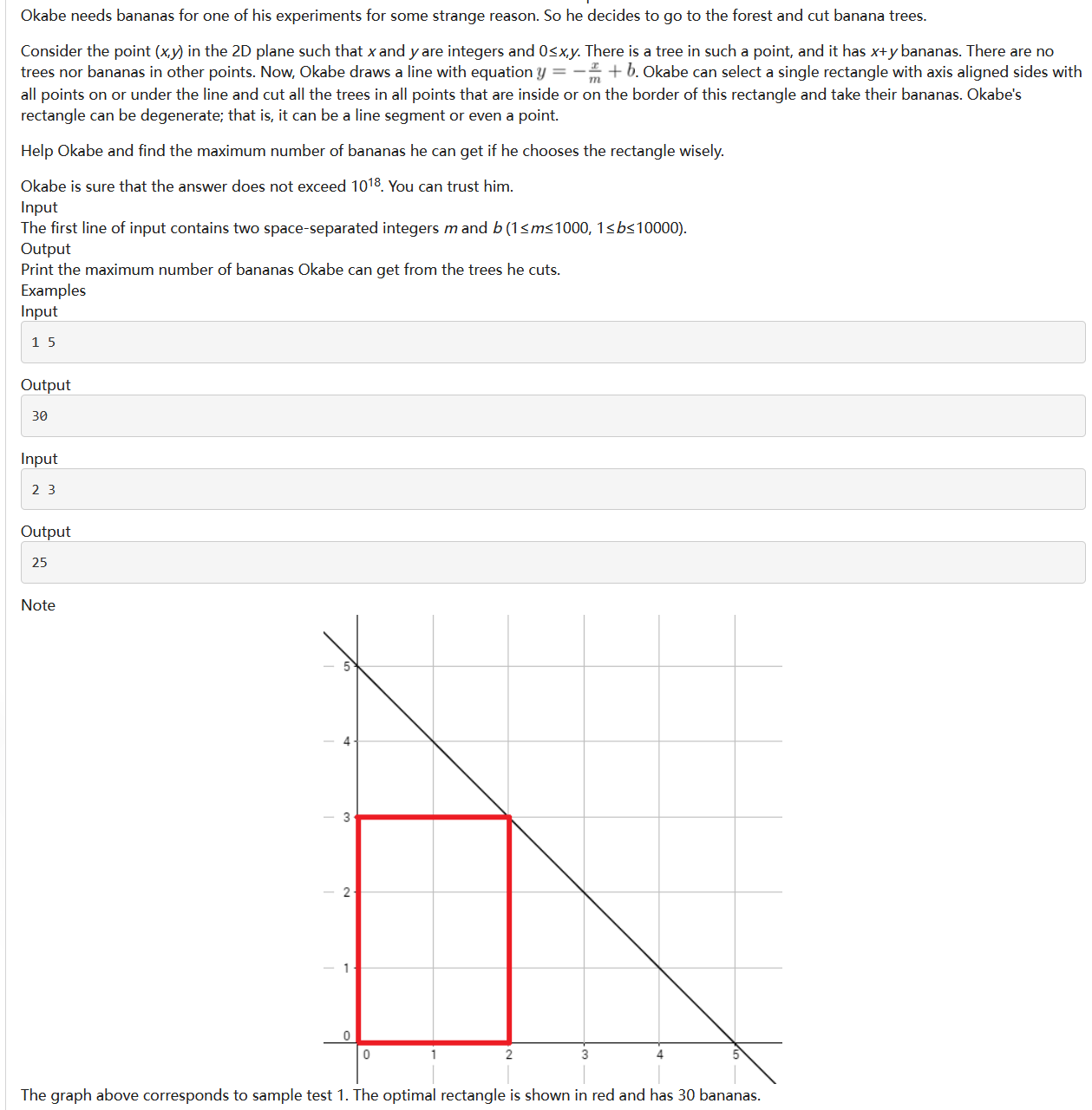
题意翻译

在整数坐标点 (x, y) 上（x ≥ 0, y ≥ 0），每个点有一棵香蕉树，树上的香蕉数量为 x + y。Okabe 画了一条直线，方程为 y = -m * x + b（其中 m 和 b 是给定的正整数）。他可以选择一个与坐标轴对齐的矩形（可以是退化的，如线段或点），该矩形包含或位于直线下方。切割该矩形内或边界上的所有树，并获得这些树上的香蕉。

题解(cpp)

对于每个矩形(0,x)(0,y)：

  • 取sumx = i * (i + 1) / 2为x方向上的总和，总共乘y+1次
  • y同理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
  long long m, b;
  long long ans = 0;
  cin >> m >> b;
  for (int i = b; i >= 0; i--)
  {
    long long sum = 0;
    long long x = m * (b - i);
    sum += (i * (i + 1) / 2) * (x + 1);
    sum += (x * (x + 1) / 2) * (i + 1);
    if (sum > ans)
      ans = sum;
  }
  cout << ans << endl;
}

J : Dynamic Problem Scoring

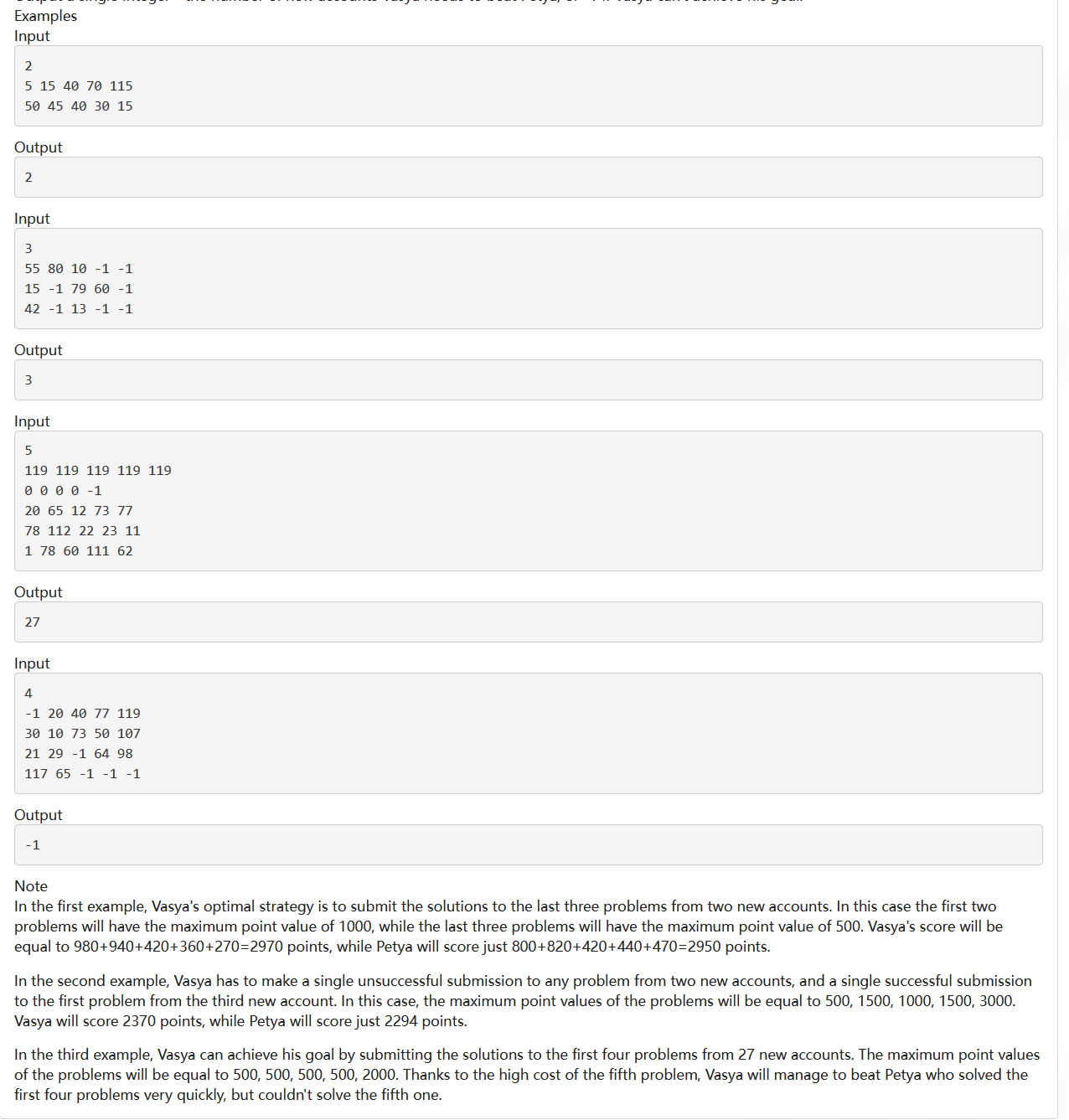
题解(cpp)

超级大模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 210;       // 最大参赛人数
const int M = 1e6;       // 考虑的最大额外参赛人数
int a[N][N];             // 二维数组存储比赛结果（参赛者×题目）
int p[5];                // 记录每道题的解出人数（0-4）
int n;                   // 实际参赛人数

// 计算某道题得分的函数
// x: 题目编号（0-4）
// m: 参赛者编号（0或1 - Vasya和Petya）
// y: 额外虚构的参赛人数
int f(int x, int m, int y)
{
  // 如果该参赛者未解出此题，返回0分
  if (a[m][x] == -1)
    return 0;
  
  int sum = 0;
  // 确定此题的基础人数
  if (a[0][x] == -1 || a[1][x] == -1 || (a[0][x] < a[1][x]))
    sum = p[x];          // Vasya解题更快或Petya未解出
  else
    sum = p[x] + y;      // Petya解题更快，计入虚构参赛者
  
  // 计算题目分值（500,1000,1500等）
  int score = 500;
  for (int i = 2; i <= 32; i <<= 1)  // i = 2,4,8,16,32
  {
    if (i * sum > (n + y))  // 检查是否超过总参赛人数
      break;
    else
      score += 500;        // 提升题目分值
  }
  
  // 计算并返回该题实际得分
  return score * (250.0 - (a[m][x])) / 250.0;
}

int main()
{
  cin >> n;  // 读取参赛人数
  
  // 读取每个参赛者的比赛结果
  for (int i = 0; i < n; i++)
  {
    for (int j = 0; j < 5; j++)
    {
      cin >> a[i][j];
      if (a[i][j] != -1)  // 如果题目被解出
        p[j]++;           // 增加该题解出计数
    }
  }
  
  int ans = 0;
  // 尝试添加1到1,000,000个虚构参赛者
  for (int i = 1; i <= M; i++)
  {
    int sv = 0, sp = 0;  // Vasya和Petya的总分
    
    // 计算Vasya的总分
    for (int k = 0; k < 5; k++)
      sv += f(k, 0, i);
    
    // 计算Petya的总分
    for (int k = 0; k < 5; k++)
      sp += f(k, 1, i);
    
    // 如果Vasya分数超过Petya，找到解
    if (sv > sp)
    {
      ans = i;
      cout << ans << endl;
      return 0;
    }
  }
  
  // 尝试1,000,000次后仍未找到解
  cout << -1 << endl;
}